Introduction - Institut de Mathématiques de Marseille
... certain “simple” Shimura varieties attached to twisted forms of unitary groups over totally real fields, and the proof in [L1] of stable cyclic base change of automorphic representations which are locally Steinberg at at least two places. These conditional results have been used successfully to prov ...
... certain “simple” Shimura varieties attached to twisted forms of unitary groups over totally real fields, and the proof in [L1] of stable cyclic base change of automorphic representations which are locally Steinberg at at least two places. These conditional results have been used successfully to prov ...
ON SYSTEMS OF DIFFERENTIAL EQUATIONS IN THE SPACE OF
... that this field is glued from linear hyperbolic fields. It will be proven in Theorem 10, that the operator L with the vector field (2) on the cylinder is normally solvable. Although the considered examples confirm our hypothesis, the question of normal solvability for such kind of fields still stays ...
... that this field is glued from linear hyperbolic fields. It will be proven in Theorem 10, that the operator L with the vector field (2) on the cylinder is normally solvable. Although the considered examples confirm our hypothesis, the question of normal solvability for such kind of fields still stays ...
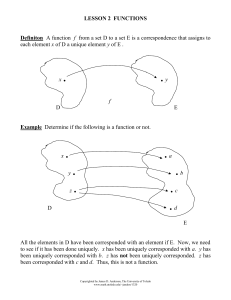
Word - The University of Toledo
... function and/or the axis of symmetry to find the x-coordinate of the vertex of the parabola. If the quadratic function has one x-intercept, then this x-intercept is the vertex of the parabola. To sketch the graph of this parabola, you would plot the vertex, which is the one x-intercept, and make the ...
... function and/or the axis of symmetry to find the x-coordinate of the vertex of the parabola. If the quadratic function has one x-intercept, then this x-intercept is the vertex of the parabola. To sketch the graph of this parabola, you would plot the vertex, which is the one x-intercept, and make the ...