POLYNOMIAL BEHAVIOUR OF KOSTKA NUMBERS
... the character χV is invariant under conjugation and hence is constant on the conjugacy classes of G. Since the diagonalizable matrices are dense in GLn , the values of χV when restricted to the diagonal matrices completely determine the character χV (since all diagonalizable matrices are, by definit ...
... the character χV is invariant under conjugation and hence is constant on the conjugacy classes of G. Since the diagonalizable matrices are dense in GLn , the values of χV when restricted to the diagonal matrices completely determine the character χV (since all diagonalizable matrices are, by definit ...
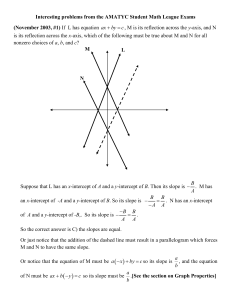
Interesting problems from the AMATYC Student Math League Exams
... From this we can conclude that a 1,3,7,21. Since b a and both are positive integers, we can disregard 1. If a 3 , then the possible values of b are 1 and 2. b 1 leads to 3 p 1 18 , which doesn’t yield an integer solution. b 2 leads to 3 p 2 18 , which doesn’t yield an integer solut ...
... From this we can conclude that a 1,3,7,21. Since b a and both are positive integers, we can disregard 1. If a 3 , then the possible values of b are 1 and 2. b 1 leads to 3 p 1 18 , which doesn’t yield an integer solution. b 2 leads to 3 p 2 18 , which doesn’t yield an integer solut ...
MATH 10021 Core Mathematics I - Department of Mathematical
... Finally, you may already know, or will soon learn, that you will be expected to do the first exam without a calculator. The idea is that the material covered will just be basic operations on real numbers, and you should know the mechanics behind all of these things. Then, later, if you wish to use a ...
... Finally, you may already know, or will soon learn, that you will be expected to do the first exam without a calculator. The idea is that the material covered will just be basic operations on real numbers, and you should know the mechanics behind all of these things. Then, later, if you wish to use a ...