Lesson 1 - Suffolk Maths
... 19. Suppose the boys name were Al, Ben, Carl. Suppose Al was the one to raise his hand. He would have reasoned as follows. "If I don't have dirt on my head then Ben or Carl raised their hands the first time because each of them saw the dirt on each other's head and didn't see any on mine. If that we ...
... 19. Suppose the boys name were Al, Ben, Carl. Suppose Al was the one to raise his hand. He would have reasoned as follows. "If I don't have dirt on my head then Ben or Carl raised their hands the first time because each of them saw the dirt on each other's head and didn't see any on mine. If that we ...
Chapter 4.6 - CS Course Webpages
... In the 19th century G. Lejuenne Dirchlet showed that every arithmetic progression ka + b, k = 1,2, …, where a and b have no common factor greater than 1 contains infinitely many primes. (The proof is beyond the scope of the text.) Are there long arithmetic progressions made up entirely of primes ...
... In the 19th century G. Lejuenne Dirchlet showed that every arithmetic progression ka + b, k = 1,2, …, where a and b have no common factor greater than 1 contains infinitely many primes. (The proof is beyond the scope of the text.) Are there long arithmetic progressions made up entirely of primes ...
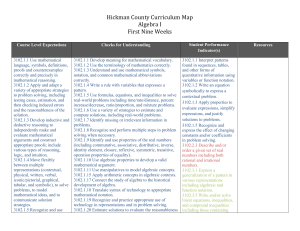
Algebra I - Hickman County Schools
... 3102.1.3 Understand and use mathematical symbols, notation, and common mathematical abbreviations correctly. 3102.1.4 Write a rule with variables that expresses a pattern. 3102.1.5 Use formulas, equations, and inequalities to solve real-world problems including time/rate/distance, percent increase/d ...
... 3102.1.3 Understand and use mathematical symbols, notation, and common mathematical abbreviations correctly. 3102.1.4 Write a rule with variables that expresses a pattern. 3102.1.5 Use formulas, equations, and inequalities to solve real-world problems including time/rate/distance, percent increase/d ...
(it), sem. -iii, logic and discrete mathematics
... This chapter consist of sets and different operations on sets with different examples which helps in better understanding of the concept and able to use in different areas. We saw the principle of inclusion – Exclusion which can be used in different counting problems we saw some concepts of number t ...
... This chapter consist of sets and different operations on sets with different examples which helps in better understanding of the concept and able to use in different areas. We saw the principle of inclusion – Exclusion which can be used in different counting problems we saw some concepts of number t ...
Mathematical Ideas
... For any set A within the universal set U, the complement of A, written A', is the set of all elements of U that are not elements of A. That is A {x | x U and x A}. ...
... For any set A within the universal set U, the complement of A, written A', is the set of all elements of U that are not elements of A. That is A {x | x U and x A}. ...
Homework #3
... and is used to detect errors in individual digits and transposition of digits. If the ISBN of a book is 0-201-57Q89-1, where Q is a digit, find Q. 1*0 + 2*2 + 3*0 + 4*1 + 5*5 + 6*7 + 7*Q + 8*8 + 9*9 + 10*1 = 0 (mod 11) That is, 230 + 7Q = 0 (mod 11) Subtracting 230 from both sides 7Q = 1 (mod 11) be ...
... and is used to detect errors in individual digits and transposition of digits. If the ISBN of a book is 0-201-57Q89-1, where Q is a digit, find Q. 1*0 + 2*2 + 3*0 + 4*1 + 5*5 + 6*7 + 7*Q + 8*8 + 9*9 + 10*1 = 0 (mod 11) That is, 230 + 7Q = 0 (mod 11) Subtracting 230 from both sides 7Q = 1 (mod 11) be ...
Addition
Addition (often signified by the plus symbol ""+"") is one of the four elementary, mathematical operations of arithmetic, with the others being subtraction, multiplication and division.The addition of two whole numbers is the total amount of those quantities combined. For example, in the picture on the right, there is a combination of three apples and two apples together; making a total of 5 apples. This observation is equivalent to the mathematical expression ""3 + 2 = 5"" i.e., ""3 add 2 is equal to 5"".Besides counting fruits, addition can also represent combining other physical objects. Using systematic generalizations, addition can also be defined on more abstract quantities, such as integers, rational numbers, real numbers and complex numbers and other abstract objects such as vectors and matrices.In arithmetic, rules for addition involving fractions and negative numbers have been devised amongst others. In algebra, addition is studied more abstractly.Addition has several important properties. It is commutative, meaning that order does not matter, and it is associative, meaning that when one adds more than two numbers, the order in which addition is performed does not matter (see Summation). Repeated addition of 1 is the same as counting; addition of 0 does not change a number. Addition also obeys predictable rules concerning related operations such as subtraction and multiplication.Performing addition is one of the simplest numerical tasks. Addition of very small numbers is accessible to toddlers; the most basic task, 1 + 1, can be performed by infants as young as five months and even some non-human animals. In primary education, students are taught to add numbers in the decimal system, starting with single digits and progressively tackling more difficult problems. Mechanical aids range from the ancient abacus to the modern computer, where research on the most efficient implementations of addition continues to this day.