Smallest Examples of Strings of Consecutive Happy Numbers
... there are at most five consecutive happy numbers beginning at N , unless N = 7899999999999959999999996 which begins a sequence of six consecutive happy numbers. Proof: Suppose N ends in the digit d0 = 6. We check for four consecutive happy numbers, that is, we check whether M1 +62 , M1 +72 , M1 +82 ...
... there are at most five consecutive happy numbers beginning at N , unless N = 7899999999999959999999996 which begins a sequence of six consecutive happy numbers. Proof: Suppose N ends in the digit d0 = 6. We check for four consecutive happy numbers, that is, we check whether M1 +62 , M1 +72 , M1 +82 ...
Medium / Short Term Maths plan
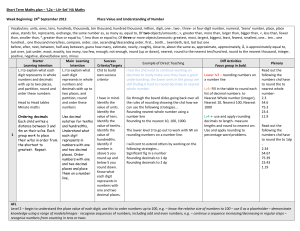
... Times table head to head and order these I have in mindOnce have explained this one explain the circle diagram and explain that on this one ...
... Times table head to head and order these I have in mindOnce have explained this one explain the circle diagram and explain that on this one ...
Lecture on Polynomial Functions
... Theorem, w(1) = 15. This theorem is important because it reveals a method for finding roots discussed below. Imaginary Roots Theorem: Imaginary roots of polynomials with real coefficients, if they exist, occur in conjugate pairs. Since this course deals only with polynomials with real coefficients, ...
... Theorem, w(1) = 15. This theorem is important because it reveals a method for finding roots discussed below. Imaginary Roots Theorem: Imaginary roots of polynomials with real coefficients, if they exist, occur in conjugate pairs. Since this course deals only with polynomials with real coefficients, ...
Induction
... We prove by induction on the number of horses that all horses have the same color. The smallest group of horses is a group of one horse. Since we usually write our predicate P so that P (0) corresponds to the base case, we define P (n) as “All horses in a group of n + 1 horses have the same color.” ...
... We prove by induction on the number of horses that all horses have the same color. The smallest group of horses is a group of one horse. Since we usually write our predicate P so that P (0) corresponds to the base case, we define P (n) as “All horses in a group of n + 1 horses have the same color.” ...
Document
... arrow is the absolute value of the number. An arrow pointing to the left is a negative number. An arrow pointing to the right is a positive number. The placement of the arrow along the number line does not matter - only the length and direction of the arrow matter. The number 7 represented as an arr ...
... arrow is the absolute value of the number. An arrow pointing to the left is a negative number. An arrow pointing to the right is a positive number. The placement of the arrow along the number line does not matter - only the length and direction of the arrow matter. The number 7 represented as an arr ...
Full text
... identities, however; are mostly "pure"-containing terms within the same family; that is, not many of them are relations that involve a Fibonacci-type sequence together with some other classical sequence having different properties. The family of Fibonacci-like numbers, for example, satisfies simple ...
... identities, however; are mostly "pure"-containing terms within the same family; that is, not many of them are relations that involve a Fibonacci-type sequence together with some other classical sequence having different properties. The family of Fibonacci-like numbers, for example, satisfies simple ...