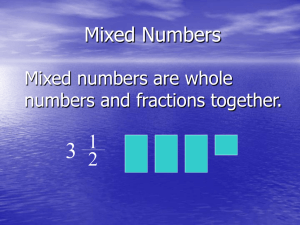Real algebraic numbers and polynomial systems
... basic operations for software libraries supporting geometric computing, such as esolid [18], exacus 2 , and the upcoming algebraic kernel of cgal 3 [10]. Our work also provides a special-purpose quantifier elimination method for one or two variables, and for parametric polynomial equalities and ine ...
... basic operations for software libraries supporting geometric computing, such as esolid [18], exacus 2 , and the upcoming algebraic kernel of cgal 3 [10]. Our work also provides a special-purpose quantifier elimination method for one or two variables, and for parametric polynomial equalities and ine ...
Unit 1 Operations with Rational Numbers Math 7
... Solve multi‐step real‐life and mathematical problems posed with positive and negative rational numbers in any form (whole numbers, fractions, and decimals), using tools strategically. Apply properties of operations to calculate with numbers in any form; convert between forms as appropriate; and asse ...
... Solve multi‐step real‐life and mathematical problems posed with positive and negative rational numbers in any form (whole numbers, fractions, and decimals), using tools strategically. Apply properties of operations to calculate with numbers in any form; convert between forms as appropriate; and asse ...
a n = n - El Camino College
... A sequence is a set of numbers written in a specific order: a1, a2, a3, a4, …, an, … • The number a1 is called the first term, a2 is the second term, and in general an is the nth term. • Since for every natural number n, there is a corresponding number an, we can define a sequence as a function. ...
... A sequence is a set of numbers written in a specific order: a1, a2, a3, a4, …, an, … • The number a1 is called the first term, a2 is the second term, and in general an is the nth term. • Since for every natural number n, there is a corresponding number an, we can define a sequence as a function. ...
Full text
... In 1960, W. Sierpiński (see [4]) showed that there are infinitely many odd positive integers k such that 2n k + 1 is composite for all n. In 1962, J. Selfridge showed that k = 78557 is a Sierpiński number. This is now believed to be the smallest Sierpiński number. As of the writing of this paper, ...
... In 1960, W. Sierpiński (see [4]) showed that there are infinitely many odd positive integers k such that 2n k + 1 is composite for all n. In 1962, J. Selfridge showed that k = 78557 is a Sierpiński number. This is now believed to be the smallest Sierpiński number. As of the writing of this paper, ...
Full text
... (ICT1)^ = ar + lO" 1 ^.! +-..- + (lO-1)"-1^ + ( K T 1 ) ^ (mod 5), fr« = /w(mod,s). Now r = 10"1 (mod5) => 10/ = l(mods) => j|(10^-1) =>zs = lOt-1 for some Z G Z . Hence, I0t~zs= 1, which implies (s, 0 = 1The statement / r n = m (mod 5) allows us to conclude that s\ n => s\m; with the additional fac ...
... (ICT1)^ = ar + lO" 1 ^.! +-..- + (lO-1)"-1^ + ( K T 1 ) ^ (mod 5), fr« = /w(mod,s). Now r = 10"1 (mod5) => 10/ = l(mods) => j|(10^-1) =>zs = lOt-1 for some Z G Z . Hence, I0t~zs= 1, which implies (s, 0 = 1The statement / r n = m (mod 5) allows us to conclude that s\ n => s\m; with the additional fac ...
14(2)
... the examples given are /7-dimensional Bernoulli and Euler numbers which are useful in the expansion in series of functions in n variables. The methods and notations introduced here will be used in the study of functions and series in $n that will be the subject of future investigations. 2. iOTATiOW ...
... the examples given are /7-dimensional Bernoulli and Euler numbers which are useful in the expansion in series of functions in n variables. The methods and notations introduced here will be used in the study of functions and series in $n that will be the subject of future investigations. 2. iOTATiOW ...
Yet another triangle for the Genocchi numbers
... According to Kreweras [11, p. 53], H2n+1 also counts the number of permutations satisfying (1) and beginning with n or n + 1. For example, H5 = S52 = 2, corresponding to the fact that exactly two of the permutations in (2) begin with 2 or 3. In [7], Dumont and Viennot gave a combinatorial interpreta ...
... According to Kreweras [11, p. 53], H2n+1 also counts the number of permutations satisfying (1) and beginning with n or n + 1. For example, H5 = S52 = 2, corresponding to the fact that exactly two of the permutations in (2) begin with 2 or 3. In [7], Dumont and Viennot gave a combinatorial interpreta ...
Full text
... Theorem 1(a) where k(p) = p − 1 and also the half-maximal period k(p) = p + 1 from (b). Despite the fact that Theorem 1 provides a great deal of information about k(m), there remain unresolved issues. In particular, while much is known about k(pe ), it is conjectured that k(p2 ) = pk(p) for all prim ...
... Theorem 1(a) where k(p) = p − 1 and also the half-maximal period k(p) = p + 1 from (b). Despite the fact that Theorem 1 provides a great deal of information about k(m), there remain unresolved issues. In particular, while much is known about k(pe ), it is conjectured that k(p2 ) = pk(p) for all prim ...
Smallest Examples of Strings of Consecutive Happy Numbers
... there are at most five consecutive happy numbers beginning at N , unless N = 7899999999999959999999996 which begins a sequence of six consecutive happy numbers. Proof: Suppose N ends in the digit d0 = 6. We check for four consecutive happy numbers, that is, we check whether M1 +62 , M1 +72 , M1 +82 ...
... there are at most five consecutive happy numbers beginning at N , unless N = 7899999999999959999999996 which begins a sequence of six consecutive happy numbers. Proof: Suppose N ends in the digit d0 = 6. We check for four consecutive happy numbers, that is, we check whether M1 +62 , M1 +72 , M1 +82 ...