PDF
... as the theorem states. For example, the sum of the first four cubes is 1 + 9 + 27 + 64 = 100. This is also equal to 1 + 3 + 5 + 7 + 9 + 11 + 13 + 17 + 19 = 100. The square root of 100 is 10, the fourth triangular number, and indeed 10 = 1 + 2 + 3 + ...
... as the theorem states. For example, the sum of the first four cubes is 1 + 9 + 27 + 64 = 100. This is also equal to 1 + 3 + 5 + 7 + 9 + 11 + 13 + 17 + 19 = 100. The square root of 100 is 10, the fourth triangular number, and indeed 10 = 1 + 2 + 3 + ...
The Fibonacci Numbers And An Unexpected Calculation.
... decimal expansion has the property that every digit is a prime number (2,3,5, or 7) is uncountable. E.g., 0.2375 and 0.55555… are in the set, but 0.145555… and 0.3030303… are not. ...
... decimal expansion has the property that every digit is a prime number (2,3,5, or 7) is uncountable. E.g., 0.2375 and 0.55555… are in the set, but 0.145555… and 0.3030303… are not. ...
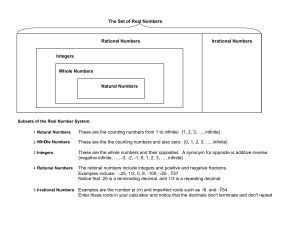
Section 2.1: The Real Number Line
... Any number that cannot be represented as a fraction. Any decimal that goes on forever with no pattern. Examples: √2, √3, ℮, π ...
... Any number that cannot be represented as a fraction. Any decimal that goes on forever with no pattern. Examples: √2, √3, ℮, π ...
Inequalities (65.1 KB)
... Inequalities (i.e., expressions involving the signs > (”is greater than”) or < (”is less than”) are readily visualised geometrically on the real number line (e.g., 4 > 3, 1 12 < 2). The aspects featured in the following two examples are important. ...
... Inequalities (i.e., expressions involving the signs > (”is greater than”) or < (”is less than”) are readily visualised geometrically on the real number line (e.g., 4 > 3, 1 12 < 2). The aspects featured in the following two examples are important. ...
1. If f(x) = 4x 2- 2x - 1, then f (1/2) equals a. 1 b.
... 10. In a sequence of six numbers, the first number is 4 and the last number is 47. Each number after the second equals the sum of the previous two numbers. If S is the sum of the six numbers in this sequence, then S lies in the interval. a. 51 to 90 ...
... 10. In a sequence of six numbers, the first number is 4 and the last number is 47. Each number after the second equals the sum of the previous two numbers. If S is the sum of the six numbers in this sequence, then S lies in the interval. a. 51 to 90 ...
Special Number Sequences Square Numbers 1 4 9 16 25 36 49 64
... Can you draw a triangle of dots for each triangle number? Here is the triangle number 15: o o o o o ...
... Can you draw a triangle of dots for each triangle number? Here is the triangle number 15: o o o o o ...
The Fibonacci Sequence
... The third month, the first pair creates another pair (so there are 3 pairs now). The fourth month the first 2 create new pairs (so 5 exist now). Etc. ...
... The third month, the first pair creates another pair (so there are 3 pairs now). The fourth month the first 2 create new pairs (so 5 exist now). Etc. ...
Unit 1 Chapter 2 (Number systems)
... 2.1 Sets of number Important sets which we meet in elementary mathematics are sets of numbers. Of particular importance, especially in analysis, is the set of real number which is denoted by R. The set of real numbers and its properties is called the real number system. 2.1.1 List of numbers: Take a ...
... 2.1 Sets of number Important sets which we meet in elementary mathematics are sets of numbers. Of particular importance, especially in analysis, is the set of real number which is denoted by R. The set of real numbers and its properties is called the real number system. 2.1.1 List of numbers: Take a ...