Transcendental vs. Algebraic Numbers
... • Mathematicians were slowly understanding the relation that the area under the rectangular hyperbola from 1 to e is 1, which makes e the base of natural logs (1, pg 1) • Huygens defined the curve y = kax, which he called logarithmic, and he estimates log10 e to 17 places (1, pg 1) • In 1668 Mercato ...
... • Mathematicians were slowly understanding the relation that the area under the rectangular hyperbola from 1 to e is 1, which makes e the base of natural logs (1, pg 1) • Huygens defined the curve y = kax, which he called logarithmic, and he estimates log10 e to 17 places (1, pg 1) • In 1668 Mercato ...
PDF
... Theorem. Given a Mersenne number m = 2n − 1 (with n a nonnegative integer), the Collatz sequence starting with m reaches 3n − 1 in precisely 2n steps. Also, the parity of such a sequence consistenly alternates parity until 3n − 1 is reached. For example, given 22 − 1 = 3 gives the Collatz sequence 3 ...
... Theorem. Given a Mersenne number m = 2n − 1 (with n a nonnegative integer), the Collatz sequence starting with m reaches 3n − 1 in precisely 2n steps. Also, the parity of such a sequence consistenly alternates parity until 3n − 1 is reached. For example, given 22 − 1 = 3 gives the Collatz sequence 3 ...
Document
... Definition: Two sets A and B have the same cardinality if and only if there exists a bijection (or a one-to-one correspondence) between them, A ~ B. We split infinite sets into two groups: 1. Sets with the same cardinality as the set of natural numbers 2. Sets with different cardinality as the set o ...
... Definition: Two sets A and B have the same cardinality if and only if there exists a bijection (or a one-to-one correspondence) between them, A ~ B. We split infinite sets into two groups: 1. Sets with the same cardinality as the set of natural numbers 2. Sets with different cardinality as the set o ...
Lecture 3
... 2 are all defined. Defining R takes some work. It turns out that R is ‘essentially’ the unique set of numbers which satisfies (P1) - (P12) together with an additional axiom (P13) which ensures there are ‘no holes’ or ‘gaps’ in our number line. This will be discussed in later lectures. Definition (3. ...
... 2 are all defined. Defining R takes some work. It turns out that R is ‘essentially’ the unique set of numbers which satisfies (P1) - (P12) together with an additional axiom (P13) which ensures there are ‘no holes’ or ‘gaps’ in our number line. This will be discussed in later lectures. Definition (3. ...
PDF
... The endless decimal notations (6) and others are, in fact, limit notations — no finite amount of decimals in them suffices to give their exact values. Remark 2. In both of the above examples, no of the sequence members was equal to the limit, but it does not need always to be so; thus for example 1+ ...
... The endless decimal notations (6) and others are, in fact, limit notations — no finite amount of decimals in them suffices to give their exact values. Remark 2. In both of the above examples, no of the sequence members was equal to the limit, but it does not need always to be so; thus for example 1+ ...
PDF
... and going to the edge. But it would be much simpler to make just two cuts to cut it into four pieces. The maximum number of pieces that can be created with a given number of cuts n is given by the formula n2 + n + 2 ...
... and going to the edge. But it would be much simpler to make just two cuts to cut it into four pieces. The maximum number of pieces that can be created with a given number of cuts n is given by the formula n2 + n + 2 ...
M098 Carson Elementary and Intermediate Algebra 3e Chapter 1 Review
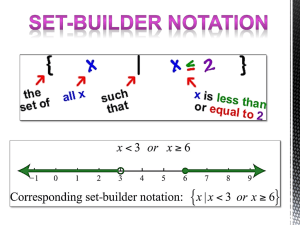
... operations that describes a calculation A mathematical relationship that contains an equal sign A mathematical relationship that contains an inequality symbol (≠, <, >, ≤, ≥) A collection of objects. The symbols used to write a set. All of the numbers represented by the number line Any real number t ...
... operations that describes a calculation A mathematical relationship that contains an equal sign A mathematical relationship that contains an inequality symbol (≠, <, >, ≤, ≥) A collection of objects. The symbols used to write a set. All of the numbers represented by the number line Any real number t ...
Chapter 2 Hints and Solutions to Exercises p
... Do a similar analysis for 3k and 3k+2. Step 2: Assume that a and b in the Pythagorean Theorem are both not multiples of 3. For all cases where this is so, derive a contradiction showing that c cannot be obtained since a 2 b 2 does not give a perfect square. For example, if a 3m 1 and b 3n ...
... Do a similar analysis for 3k and 3k+2. Step 2: Assume that a and b in the Pythagorean Theorem are both not multiples of 3. For all cases where this is so, derive a contradiction showing that c cannot be obtained since a 2 b 2 does not give a perfect square. For example, if a 3m 1 and b 3n ...
Factors and multiples 10a Square numbers 10b
... 2 List all the factors of these numbers. a 3 b 4 c 10 d 18 e 25 3 True or false? Explain each answer. a 38 is an even number b 85 is a multiple of 5 c 4 is a factor of 34 d 72 will divide by 3 exactly. 4 Gemma wins £68.43 on the lottery. She decides to give an equal share to each of her three childr ...
... 2 List all the factors of these numbers. a 3 b 4 c 10 d 18 e 25 3 True or false? Explain each answer. a 38 is an even number b 85 is a multiple of 5 c 4 is a factor of 34 d 72 will divide by 3 exactly. 4 Gemma wins £68.43 on the lottery. She decides to give an equal share to each of her three childr ...