Floating Point 1()
... Converting Decimal to FP (2/3) • Not So Simple Case: If denominator is not an exponent of 2. • Then we can’t represent number precisely, but that’s why we have so many bits in significand: for precision • Once we have significand, normalizing a number to get the exponent is easy. • So how do we get ...
... Converting Decimal to FP (2/3) • Not So Simple Case: If denominator is not an exponent of 2. • Then we can’t represent number precisely, but that’s why we have so many bits in significand: for precision • Once we have significand, normalizing a number to get the exponent is easy. • So how do we get ...
Provo City School District Mathematics Resources 1 Table of
... In grade 2, instructional time should focus on four critical areas: (1) extending understanding of baseten notation; (2) building fluency with addition and subtraction; (3) using standard units of measure; and (4) describing and analyzing shapes. Operations and Algebraic Thinking (2.OA) A. Represent ...
... In grade 2, instructional time should focus on four critical areas: (1) extending understanding of baseten notation; (2) building fluency with addition and subtraction; (3) using standard units of measure; and (4) describing and analyzing shapes. Operations and Algebraic Thinking (2.OA) A. Represent ...
Theory Behind RSA
... of p1, p2, …, pk, so must be divisible by a prime not on the list. The largest known prime is 213,466,917-1, which has 4,053,946 digits Primality: Simply start checking for divisibility by 2, 3, 4, 5, 6, 7, … A number n is prime if it isn’t divisible by any number up to n Determining whether ...
... of p1, p2, …, pk, so must be divisible by a prime not on the list. The largest known prime is 213,466,917-1, which has 4,053,946 digits Primality: Simply start checking for divisibility by 2, 3, 4, 5, 6, 7, … A number n is prime if it isn’t divisible by any number up to n Determining whether ...
Periodicity and Correlation Properties of d
... S to the t-shift of T, bit by bit modulo 2. Recently Klapper and Goresky [12] the authors considered a slightly different notion of cross-correlation between sequences: the arithmetic cross-correlation (with shift t) of S and T is the number of ones minus the number of zeroes in one period of (the p ...
... S to the t-shift of T, bit by bit modulo 2. Recently Klapper and Goresky [12] the authors considered a slightly different notion of cross-correlation between sequences: the arithmetic cross-correlation (with shift t) of S and T is the number of ones minus the number of zeroes in one period of (the p ...
Tau Numbers: A Partial Proof of a Conjecture and Other Results
... Dirichlet’s Theorem states that when gcd(a, b) = 1 then the set {n : an + b is prime} is infinite. This theorem is equivalent to there being an infinite number of primes in any arithmetic progression aside from certain trivial cases. For tau numbers the equivalent problem becomes: Conjecture 32. An ...
... Dirichlet’s Theorem states that when gcd(a, b) = 1 then the set {n : an + b is prime} is infinite. This theorem is equivalent to there being an infinite number of primes in any arithmetic progression aside from certain trivial cases. For tau numbers the equivalent problem becomes: Conjecture 32. An ...
Chapter 20 Electrochemistry
... • If a reaction occurs in basic solution, one can balance it as if it occurred in acid. • Once the equation is balanced, add OH− to each side to “neutralize” the H+ in the equation and create water in its place. • If this produces water on both sides, you might have to subtract water from each side. ...
... • If a reaction occurs in basic solution, one can balance it as if it occurred in acid. • Once the equation is balanced, add OH− to each side to “neutralize” the H+ in the equation and create water in its place. • If this produces water on both sides, you might have to subtract water from each side. ...
Integers and Algorithms - School of Computing Science
... Therefore, the divisor a or b is either prime or due to the fundamental theorem of arithmetic, can be expressed as a product of primes ...
... Therefore, the divisor a or b is either prime or due to the fundamental theorem of arithmetic, can be expressed as a product of primes ...
$doc.title
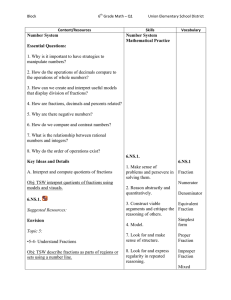
... percents using a variety of methods. Interpret and model quotients of fractions through the creation of story contexts.[1] ( 6.NS.1) Compute quotients of fractions.[1] ( 6.NS.1) Solve word problems involving division of fractions by fractions, e.g., by using visual fraction models and equations to r ...
... percents using a variety of methods. Interpret and model quotients of fractions through the creation of story contexts.[1] ( 6.NS.1) Compute quotients of fractions.[1] ( 6.NS.1) Solve word problems involving division of fractions by fractions, e.g., by using visual fraction models and equations to r ...
Elementary mathematics
Elementary mathematics consists of mathematics topics frequently taught at the primary or secondary school levels. The most basic topics in elementary mathematics are arithmetic and geometry. Beginning in the last decades of the 20th century, there has been an increased emphasis on problem solving. Elementary mathematics is used in everyday life in such activities as making change, cooking, buying and selling stock, and gambling. It is also an essential first step on the path to understanding science.In secondary school, the main topics in elementary mathematics are algebra and trigonometry. Calculus, even though it is often taught to advanced secondary school students, is usually considered college level mathematics.