Notes - IMSc
... P1. If `0i ≤ `i , i = 1, . . . , r, then n → (`1 , . . . , `r ) implies n → (`01 , . . . , `0r ). Clearly, if there is a monochromatic K`i , then all induced subgraphs of it of size `0i are monochromatic as well. P2. If m ≥ n and n → (`1 , . . . , `r ) then m → (`1 , . . . , `r ). This is obvious, ...
... P1. If `0i ≤ `i , i = 1, . . . , r, then n → (`1 , . . . , `r ) implies n → (`01 , . . . , `0r ). Clearly, if there is a monochromatic K`i , then all induced subgraphs of it of size `0i are monochromatic as well. P2. If m ≥ n and n → (`1 , . . . , `r ) then m → (`1 , . . . , `r ). This is obvious, ...
Simple Continued Fractions for Some Irrational Numbers
... fraction expansion is infinite and periodic after some point. We will show that the assumption that the continued fraction for B(u, ∞) is periodic after some point leads to a contradiction. Assume that the length of the repeating portion is r terms. We may also assume without loss of generality that ...
... fraction expansion is infinite and periodic after some point. We will show that the assumption that the continued fraction for B(u, ∞) is periodic after some point leads to a contradiction. Assume that the length of the repeating portion is r terms. We may also assume without loss of generality that ...
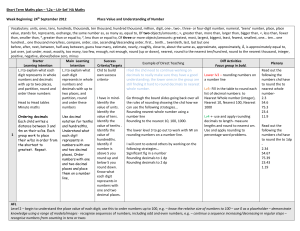
Medium / Short Term Maths plan
... Level 2 – begin to understand the place value of each digit; use this to order numbers up to 100, e.g. – know the relative size of numbers to 100 – use 0 as a placeholder – demonstrate knowledge using a range of models/images · recognise sequences of numbers, including odd and even numbers, e.g. – c ...
... Level 2 – begin to understand the place value of each digit; use this to order numbers up to 100, e.g. – know the relative size of numbers to 100 – use 0 as a placeholder – demonstrate knowledge using a range of models/images · recognise sequences of numbers, including odd and even numbers, e.g. – c ...
Honors Pre-Calc Unit 2 Test
... **4. Use the conjugate of the denominator to write in standard form: 2 3i **5. Divide x5 + 3 x4 –2 x – 1 by x – 3 *6. Divide (9x3 – 18x2 – x + 2) by (3x + 1) **7. Multiply and simplify completely: (3 -2i)(5 + i) – 6i. *8. Plot the number 3 – 2i on the complex plane. (Sketch the real and imaginary ...
... **4. Use the conjugate of the denominator to write in standard form: 2 3i **5. Divide x5 + 3 x4 –2 x – 1 by x – 3 *6. Divide (9x3 – 18x2 – x + 2) by (3x + 1) **7. Multiply and simplify completely: (3 -2i)(5 + i) – 6i. *8. Plot the number 3 – 2i on the complex plane. (Sketch the real and imaginary ...
Real Numbers Assignment 7
... the decimal expansion of a has non-terminating repeating decimal expansion. ...
... the decimal expansion of a has non-terminating repeating decimal expansion. ...
Throughout time numbers and their seemingly magical properties
... numbers are derived in the same manner as the Fibonacci numbers, but the first two numbers are 2 and 1 producing the following numbers: ...
... numbers are derived in the same manner as the Fibonacci numbers, but the first two numbers are 2 and 1 producing the following numbers: ...
Exponential Functions
... If b is any positive number, then the expression bx designates exactly one real number for every real value of x. Therefore the equation f(x) = bx defines a function whose domain is the set of real numbers. Furthermore, if we add the restriction b 1, then any equation of the form f(x) = bx describ ...
... If b is any positive number, then the expression bx designates exactly one real number for every real value of x. Therefore the equation f(x) = bx defines a function whose domain is the set of real numbers. Furthermore, if we add the restriction b 1, then any equation of the form f(x) = bx describ ...
Module Overview
... Rationalize the Denominator- Dividing by a Square Root that is not a perfect square Rationalize the Denominator Notice that after simplifying the radical, we still have a square root in the denominator. We cannot leave a square root on the bottom of a fraction, so we have to find a way to get rid o ...
... Rationalize the Denominator- Dividing by a Square Root that is not a perfect square Rationalize the Denominator Notice that after simplifying the radical, we still have a square root in the denominator. We cannot leave a square root on the bottom of a fraction, so we have to find a way to get rid o ...
Elementary mathematics
Elementary mathematics consists of mathematics topics frequently taught at the primary or secondary school levels. The most basic topics in elementary mathematics are arithmetic and geometry. Beginning in the last decades of the 20th century, there has been an increased emphasis on problem solving. Elementary mathematics is used in everyday life in such activities as making change, cooking, buying and selling stock, and gambling. It is also an essential first step on the path to understanding science.In secondary school, the main topics in elementary mathematics are algebra and trigonometry. Calculus, even though it is often taught to advanced secondary school students, is usually considered college level mathematics.