Equivalence Relations
... Equivalence relations The concept of equivalence relation is an abstraction of the idea of two math objects being like each other in some respect. If an object a is like an object b in some specified way, then b is like a in that respect. a is like itself in every respect! So if you want to give ...
... Equivalence relations The concept of equivalence relation is an abstraction of the idea of two math objects being like each other in some respect. If an object a is like an object b in some specified way, then b is like a in that respect. a is like itself in every respect! So if you want to give ...
Elementary Number Theory
... where mj , nj are non-negative integers, possibly equal to 0. If we have mj ≤ nj for all j, then m obviously divides n, since the quotient of m/n is a product of primes, hence an integer. The inverse is also true. If m divides n, then n/m has prime factorization pn1 1 −n1 · · · pnr r −mr , and since ...
... where mj , nj are non-negative integers, possibly equal to 0. If we have mj ≤ nj for all j, then m obviously divides n, since the quotient of m/n is a product of primes, hence an integer. The inverse is also true. If m divides n, then n/m has prime factorization pn1 1 −n1 · · · pnr r −mr , and since ...
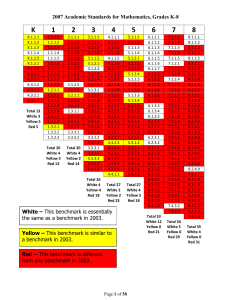
Standards with notes regarding 2003 Standards
... of faces, and the number of sides, edges and vertices describe and (corners). compare basic 2.3.1.2 Identify and name basic two- and three-dimensional shapes shapes, such as squares, circles, triangles, rectangles, according to trapezoids, hexagons, cubes, rectangular prisms, their geometric cones, ...
... of faces, and the number of sides, edges and vertices describe and (corners). compare basic 2.3.1.2 Identify and name basic two- and three-dimensional shapes shapes, such as squares, circles, triangles, rectangles, according to trapezoids, hexagons, cubes, rectangular prisms, their geometric cones, ...
Sets, Infinity, and Mappings - University of Southern California
... Thus, starting with the infinite set N, the power set operation iteratively produces new infinite sets with strictly larger cardinality than all of their predecessors. H. A deep paradox The chain of sets given in (2) shows there are infinitely many levels of infinity. That is, there are infinitely m ...
... Thus, starting with the infinite set N, the power set operation iteratively produces new infinite sets with strictly larger cardinality than all of their predecessors. H. A deep paradox The chain of sets given in (2) shows there are infinitely many levels of infinity. That is, there are infinitely m ...
Fifty Lectures for SAT And PSAT Math (9) Factors
... Example 2: How many factors does 23 · 36 · 5 have? Solution: 56 factors. The number of factors is (3 + 1)(6 + 1)(1 + 1) = 56. Example 3: How many distinct positive integral factors would the following product have: ...
... Example 2: How many factors does 23 · 36 · 5 have? Solution: 56 factors. The number of factors is (3 + 1)(6 + 1)(1 + 1) = 56. Example 3: How many distinct positive integral factors would the following product have: ...
MT1
... {(p, q): p p, q q} belongs to: (a) P Q (b) P Q (c) P – Q (d) P × Q If order pairs (x+2, 4) = 4, y–2) then value of x, y is respectively: (a) 2, 4 (b) 2, 2 (c) 2, 6 (d) 6, 2 The set of all second elements in a relation R from a set A to B is called the _______ of R. (a) Domain (b) Range (c) C ...
... {(p, q): p p, q q} belongs to: (a) P Q (b) P Q (c) P – Q (d) P × Q If order pairs (x+2, 4) = 4, y–2) then value of x, y is respectively: (a) 2, 4 (b) 2, 2 (c) 2, 6 (d) 6, 2 The set of all second elements in a relation R from a set A to B is called the _______ of R. (a) Domain (b) Range (c) C ...
3/3/06
... 2 whole times with a remainder of 2. This means that the x on the outside has a power of 3 and the x on the inside has a power of 2. Similarly, the exponent on the y is 5 and 3 goes into it 1 whole time with 2 left over. ...
... 2 whole times with a remainder of 2. This means that the x on the outside has a power of 3 and the x on the inside has a power of 2. Similarly, the exponent on the y is 5 and 3 goes into it 1 whole time with 2 left over. ...
10/27/04
... N • two’s complement • It is simple to determine the representation of a negative number in ones complement given the positive • It is easy to convert a ones complement representation to a twos complement representation by simply adding ...
... N • two’s complement • It is simple to determine the representation of a negative number in ones complement given the positive • It is easy to convert a ones complement representation to a twos complement representation by simply adding ...
Guess Paper – 2012 Class – X Subject – Mathematics REAL
... ii. A friction becomes when 1 is subtracted from the numerator and it becomes when ...
... ii. A friction becomes when 1 is subtracted from the numerator and it becomes when ...
CS 413, Assignment 1
... 4. The components of a knapsack problem are shown. Give the mathematical expression (equation) showing their relationship, assuming that the vector V is a solution. V = (v1, v2, …, vn), vi an element of {0, 1) S = (a1, a2, …, an), ai an element of {the positive integers) T, a positive integer 5. Her ...
... 4. The components of a knapsack problem are shown. Give the mathematical expression (equation) showing their relationship, assuming that the vector V is a solution. V = (v1, v2, …, vn), vi an element of {0, 1) S = (a1, a2, …, an), ai an element of {the positive integers) T, a positive integer 5. Her ...
Elementary mathematics
Elementary mathematics consists of mathematics topics frequently taught at the primary or secondary school levels. The most basic topics in elementary mathematics are arithmetic and geometry. Beginning in the last decades of the 20th century, there has been an increased emphasis on problem solving. Elementary mathematics is used in everyday life in such activities as making change, cooking, buying and selling stock, and gambling. It is also an essential first step on the path to understanding science.In secondary school, the main topics in elementary mathematics are algebra and trigonometry. Calculus, even though it is often taught to advanced secondary school students, is usually considered college level mathematics.