Elementary Number Theory
... 5. Are there infinitely many primes of the form 22 + 1? Primes of this form are called Fermat primes. 6. (3n+1 Conjecture) Consider the function f defined for positive integers n as follows: f (n) = 3n + 1 if n is odd and f (n) = n/2 if n is even. The conjecture is that the sequence f (n), f (f (n)) ...
... 5. Are there infinitely many primes of the form 22 + 1? Primes of this form are called Fermat primes. 6. (3n+1 Conjecture) Consider the function f defined for positive integers n as follows: f (n) = 3n + 1 if n is odd and f (n) = n/2 if n is even. The conjecture is that the sequence f (n), f (f (n)) ...
From tilings by Pythagorean triangles to Dyck paths: a
... published an example of a set of multiples without natural density. In response to Besicovitch, I proved in 1948 that the set of semiperimeters of Pythagorean triangle has natural density, but at that time I didn’t known its exact value. I conjectured that this density is 1. ...
... published an example of a set of multiples without natural density. In response to Besicovitch, I proved in 1948 that the set of semiperimeters of Pythagorean triangle has natural density, but at that time I didn’t known its exact value. I conjectured that this density is 1. ...
Full text
... that there are Fk_6 paths of length k - 5 which come from the upper surface, go to plate 2/, and then to the x-dot (note that the total path would then have length k + 1, since a path of 2 + 1 would be needed to reach the #-dot and a path of 1 + 2 to leave the x-dot). There are Fk_5 paths which refl ...
... that there are Fk_6 paths of length k - 5 which come from the upper surface, go to plate 2/, and then to the x-dot (note that the total path would then have length k + 1, since a path of 2 + 1 would be needed to reach the #-dot and a path of 1 + 2 to leave the x-dot). There are Fk_5 paths which refl ...
Full text
... reduced residue classes. It should also be pointed out that the counts are not complete for the larger numbers n: we sped up calculations by using only the smallest entries from iV"init. Based on numerical evidence, this missed some but not many primes. An interesting feature to the table is that al ...
... reduced residue classes. It should also be pointed out that the counts are not complete for the larger numbers n: we sped up calculations by using only the smallest entries from iV"init. Based on numerical evidence, this missed some but not many primes. An interesting feature to the table is that al ...
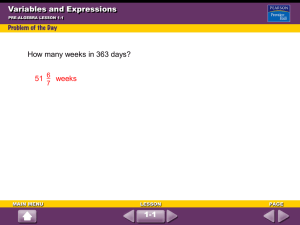
Chapter 1 - Crestwood Local Schools
... a. Write a variable expression for the number of cartons the Café should buy for x eggs. b. Evaluate the expression for 180 eggs. a. x eggs ...
... a. Write a variable expression for the number of cartons the Café should buy for x eggs. b. Evaluate the expression for 180 eggs. a. x eggs ...
Collatz conjecture

The Collatz conjecture is a conjecture in mathematics named after Lothar Collatz, who first proposed it in 1937. The conjecture is also known as the 3n + 1 conjecture, the Ulam conjecture (after Stanisław Ulam), Kakutani's problem (after Shizuo Kakutani), the Thwaites conjecture (after Sir Bryan Thwaites), Hasse's algorithm (after Helmut Hasse), or the Syracuse problem; the sequence of numbers involved is referred to as the hailstone sequence or hailstone numbers (because the values are usually subject to multiple descents and ascents like hailstones in a cloud), or as wondrous numbers.Take any natural number n. If n is even, divide it by 2 to get n / 2. If n is odd, multiply it by 3 and add 1 to obtain 3n + 1. Repeat the process (which has been called ""Half Or Triple Plus One"", or HOTPO) indefinitely. The conjecture is that no matter what number you start with, you will always eventually reach 1. The property has also been called oneness.Paul Erdős said about the Collatz conjecture: ""Mathematics may not be ready for such problems."" He also offered $500 for its solution.