Fibonacci Identities as Binomial Sums
... Finding the exact value of Fn from (2) requires multiple steps of busy and messy algebraic calculations which is not desirable. So, our goal in this note is to present Fn as a binomial sum for quick numerical calculations. Likewise, we use this binomial sum to write some well-known and fundamental i ...
... Finding the exact value of Fn from (2) requires multiple steps of busy and messy algebraic calculations which is not desirable. So, our goal in this note is to present Fn as a binomial sum for quick numerical calculations. Likewise, we use this binomial sum to write some well-known and fundamental i ...
HOSCCFractions_G3_G4_G5_SS_11 12 13
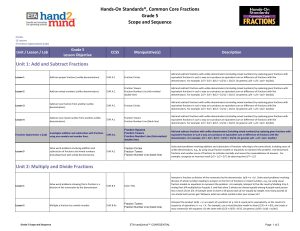
... Interpret a fraction as division of the numerator by the denominator (a/b = a ÷ b) . Solve word problems involving division of whole numbers leading to answers in the form of fractions or mixed numbers, e.g., by using visual fraction models or equations to represent the problem. For example, int ...
... Interpret a fraction as division of the numerator by the denominator (a/b = a ÷ b) . Solve word problems involving division of whole numbers leading to answers in the form of fractions or mixed numbers, e.g., by using visual fraction models or equations to represent the problem. For example, int ...
The Fundamentals: Algorithms, the Integers, and Matrices
... In the 19th century G. Lejuenne Dirchlet showed that every arithmetic progression ka + b, k = 1,2, …, where a and b have no common factor greater than 1 contains infinitely many primes. (The proof is beyond the scope of the text.) Are there long arithmetic progressions made up entirely of primes ...
... In the 19th century G. Lejuenne Dirchlet showed that every arithmetic progression ka + b, k = 1,2, …, where a and b have no common factor greater than 1 contains infinitely many primes. (The proof is beyond the scope of the text.) Are there long arithmetic progressions made up entirely of primes ...
Collatz conjecture

The Collatz conjecture is a conjecture in mathematics named after Lothar Collatz, who first proposed it in 1937. The conjecture is also known as the 3n + 1 conjecture, the Ulam conjecture (after Stanisław Ulam), Kakutani's problem (after Shizuo Kakutani), the Thwaites conjecture (after Sir Bryan Thwaites), Hasse's algorithm (after Helmut Hasse), or the Syracuse problem; the sequence of numbers involved is referred to as the hailstone sequence or hailstone numbers (because the values are usually subject to multiple descents and ascents like hailstones in a cloud), or as wondrous numbers.Take any natural number n. If n is even, divide it by 2 to get n / 2. If n is odd, multiply it by 3 and add 1 to obtain 3n + 1. Repeat the process (which has been called ""Half Or Triple Plus One"", or HOTPO) indefinitely. The conjecture is that no matter what number you start with, you will always eventually reach 1. The property has also been called oneness.Paul Erdős said about the Collatz conjecture: ""Mathematics may not be ready for such problems."" He also offered $500 for its solution.