Definite Integrals - West Virginia University
... Definite Integrals Finding areas using the Fundamental Theorem of Calculus ...
... Definite Integrals Finding areas using the Fundamental Theorem of Calculus ...
A quick review of Mathe 114
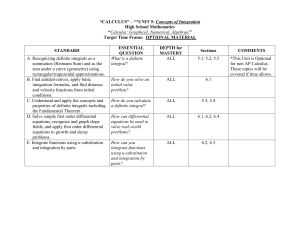
... L: local maximum/minimum values C: concavity (concave up/down intervals) Final sketching: (i). Locate a few special points: points on the x-/y- axes; local maximum/minimum value points (ii). Divide the domain of the function into many subintervals by the critical points, inflection points and those ...
... L: local maximum/minimum values C: concavity (concave up/down intervals) Final sketching: (i). Locate a few special points: points on the x-/y- axes; local maximum/minimum value points (ii). Divide the domain of the function into many subintervals by the critical points, inflection points and those ...
q-Series 1 History and q-Integers Michael Griffith
... We can see that the Jackson derivative, integral, and our ensemble of q-analogs behave altogether like classical calculus. This parallel behavior positions the q-calculus as a broadly applicable generalization of classical calculus. The tools and identities formulated in classical calculus and their ...
... We can see that the Jackson derivative, integral, and our ensemble of q-analogs behave altogether like classical calculus. This parallel behavior positions the q-calculus as a broadly applicable generalization of classical calculus. The tools and identities formulated in classical calculus and their ...
Study guide for the third exam
... In pure-time differential equations, we are given the rate of change as a function of time (such as a measured rate of change). In autonomous differential equations, we are given a rule that gives the rate of change as a function of the value of the state variable. To determine a specific solution t ...
... In pure-time differential equations, we are given the rate of change as a function of time (such as a measured rate of change). In autonomous differential equations, we are given a rule that gives the rate of change as a function of the value of the state variable. To determine a specific solution t ...
AP Calculus
... The “average” slope is the slope of a line drawn from endpoint to endpoint. No matter how much the function may change between endpoints, we say that its “average” change is simply the ratio of changes in y to changes in x. For average slope, use the slope formula. The MVT says that there has to be ...
... The “average” slope is the slope of a line drawn from endpoint to endpoint. No matter how much the function may change between endpoints, we say that its “average” change is simply the ratio of changes in y to changes in x. For average slope, use the slope formula. The MVT says that there has to be ...
Fundamental Theorem of Calculus, Riemann Sums, Substitution
... A calc student upset as could be That his antiderivative didn't agree With the one in the book E'en aft one more look. Oh! Seems he forgot to write the "+ C". -Anonymous ...
... A calc student upset as could be That his antiderivative didn't agree With the one in the book E'en aft one more look. Oh! Seems he forgot to write the "+ C". -Anonymous ...
Math 108, Final Exam Checklist
... Chapter 1: Basic properties of functions • Ways to represent functions • Domain and range of a function • Building new functions out of old ones. Composition. • Inverse of a function • Piecewise functions • Vertical and horizontal translation and stretch/squeeze • Elementary functions: Polynomials, ...
... Chapter 1: Basic properties of functions • Ways to represent functions • Domain and range of a function • Building new functions out of old ones. Composition. • Inverse of a function • Piecewise functions • Vertical and horizontal translation and stretch/squeeze • Elementary functions: Polynomials, ...
Riemann Sums Workshop Handout
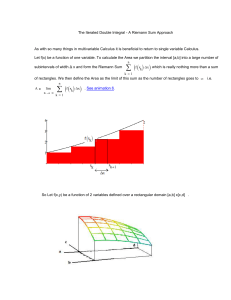
... Definition of a Riemann Sum: Consider a function f x defined on a closed interval a, b , partitioned into n subintervals of equal width by means of points a x0 x1 x 2 xn 1 xn b . On each subinterval xk 1 , xk , pick an arbitrary point xk* . Then the Riema ...
... Definition of a Riemann Sum: Consider a function f x defined on a closed interval a, b , partitioned into n subintervals of equal width by means of points a x0 x1 x 2 xn 1 xn b . On each subinterval xk 1 , xk , pick an arbitrary point xk* . Then the Riema ...
Calculus Jeopardy - Designated Deriver
... calculations of area using anti-derivatives. What is The Fundamental Theorem of Calculus? ...
... calculations of area using anti-derivatives. What is The Fundamental Theorem of Calculus? ...
Section 6.6
... The energy of motion caused by the work is called the kinetic energy of the car. There is a principle of physics called the work-energy relationship. We will barely touch on this principle. Our main goal (on later slides) is to see how integration is related. ...
... The energy of motion caused by the work is called the kinetic energy of the car. There is a principle of physics called the work-energy relationship. We will barely touch on this principle. Our main goal (on later slides) is to see how integration is related. ...
MATH 1920 --- CALCULUS II COURSE SYLLABUS INSTRUCTOR
... A grade of I will be given only in accordance with the University Policy. If you have a disability that may require assistance or accommodation, or you have questions related to any accommodations for testing, note takers, readers, etc., please speak with me as soon as possible. Students may also co ...
... A grade of I will be given only in accordance with the University Policy. If you have a disability that may require assistance or accommodation, or you have questions related to any accommodations for testing, note takers, readers, etc., please speak with me as soon as possible. Students may also co ...
Representation of One as the Sum of Unit Fractions 1 Introduction
... One is expressed as the sum of the reciprocals of a certain set of integers. We give an elegant proof to the fact applying the polynomial theorem and basic calculus. ...
... One is expressed as the sum of the reciprocals of a certain set of integers. We give an elegant proof to the fact applying the polynomial theorem and basic calculus. ...
Slide 1
... Conclusion: Since the sum of the areas of the rectangles are smaller than the area A below the graph of ...
... Conclusion: Since the sum of the areas of the rectangles are smaller than the area A below the graph of ...