Learning Area
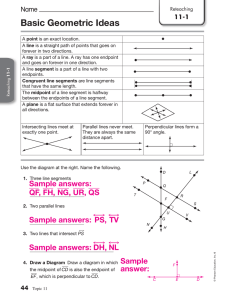
... This is an example of the line segment that could be labelled. The angles should also be marked as shown in the diagram below. That will help the learners to see the relationship clearer. There are many different versions of the shapes in question that can be found. See teacher notes for more guidan ...
... This is an example of the line segment that could be labelled. The angles should also be marked as shown in the diagram below. That will help the learners to see the relationship clearer. There are many different versions of the shapes in question that can be found. See teacher notes for more guidan ...
R2 with answers
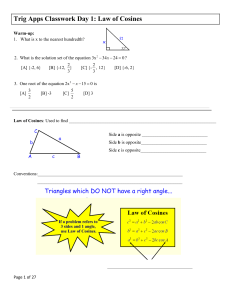
... with two different triangles, use diagrams to solve both triangles. 3. Understand how trigonometric solutions to these problems give the correct number of answers. (For either one triangle, no triangles, or two triangles.) 4. OPTIONAL: Use trigonometry to solve triangles in the “ambiguous case.” Sec ...
... with two different triangles, use diagrams to solve both triangles. 3. Understand how trigonometric solutions to these problems give the correct number of answers. (For either one triangle, no triangles, or two triangles.) 4. OPTIONAL: Use trigonometry to solve triangles in the “ambiguous case.” Sec ...
Angle Theorems - hrsbstaff.ednet.ns.ca
... Lines AB and CD are parallel to one another (hence the » on the lines). a and d are known as vertically opposite angles. Vertically opposite angles are equal. (b and c, e and h, f and g are also vertically opposite). g and c are corresponding angles. Corresponding angles are equal. (h and d, f and b ...
... Lines AB and CD are parallel to one another (hence the » on the lines). a and d are known as vertically opposite angles. Vertically opposite angles are equal. (b and c, e and h, f and g are also vertically opposite). g and c are corresponding angles. Corresponding angles are equal. (h and d, f and b ...
Perceived visual angle
In human visual perception, the visual angle, denoted θ, subtended by a viewed object sometimes looks larger or smaller than its actual value. One approach to this phenomenon posits a subjective correlate to the visual angle: the perceived visual angle or perceived angular size. An optical illusion where the physical and subjective angles differ is then called a visual angle illusion or angular size illusion.Angular size illusions are most obvious as relative angular size illusions, in which two objects that subtend the same visual angle appear to have different angular sizes; it is as if their equal-sized images on the retina were of different sizes. Angular size illusions are contrasted with linear size illusions, in which two objects that are the same physical size do not appear so. An angular size illusion may be accompanied by (or cause) a linear size illusion at the same time.The perceived visual angle paradigm begins with a rejection of the classical size–distance invariance hypothesis (SDIH), which states that the ratio of perceived linear size to perceived distance is a simple function of the visual angle. The SDIH does not explain some illusions, such as the Moon illusion, in which the Moon appears larger when it is near the horizon. It is replaced by a perceptual SDIH, in which the visual angle is replaced by the perceived visual angle. This new formulation avoids some of the paradoxes of the SDIH, but it remains difficult to explain why a given illusion occurs.This paradigm is not universally accepted; many textbook explanations of size and distance perception do not refer to the perceived visual angle, and some researchers deny that it exists. Some recent evidence supporting the idea, reported by Murray, Boyaci and Kersten (2006), suggests a direct relationship between the perceived angular size of an object and the size of the neural activity pattern it excites in the primary visual cortex.