Trigonometry
... 2. Find to the nearest degree the measure of the angle of elevation of the sun when a vertical pole 6 feet high casts a shadow 8 feet long. ...
... 2. Find to the nearest degree the measure of the angle of elevation of the sun when a vertical pole 6 feet high casts a shadow 8 feet long. ...
secondary geometry
... Ask pupils to turn through a right, acute or obtuse angle, and then to try to draw the movement they have made. Invite pupils to choose, from a collection of shapes, a shape with one right angle, two acute angles, etc. Demonstrate the comparison with right angles (that is, greater than or less than ...
... Ask pupils to turn through a right, acute or obtuse angle, and then to try to draw the movement they have made. Invite pupils to choose, from a collection of shapes, a shape with one right angle, two acute angles, etc. Demonstrate the comparison with right angles (that is, greater than or less than ...
Teacher Notes PDF - TI Education
... essential activity for the understanding of geometry. In this activity, you will begin with an exploration of interior angles but will then investigate relationships between interior and exterior angles of a triangle. This activity makes use of the following definitions: Interior angles — angles for ...
... essential activity for the understanding of geometry. In this activity, you will begin with an exploration of interior angles but will then investigate relationships between interior and exterior angles of a triangle. This activity makes use of the following definitions: Interior angles — angles for ...
Honors Geometry Unit 1 Exam Review Review your Homework
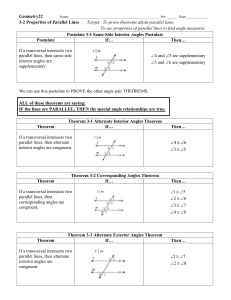
... Write two-column proofs to prove theorems about lines and angles. Complete two-column proofs to prove theorems about segments. Complete two-column proofs to prove theorems about angles. Make conjectures about the angles formed by a pair of parallel lines and a transversal. Prove theorems about the a ...
... Write two-column proofs to prove theorems about lines and angles. Complete two-column proofs to prove theorems about segments. Complete two-column proofs to prove theorems about angles. Make conjectures about the angles formed by a pair of parallel lines and a transversal. Prove theorems about the a ...
Perceived visual angle
In human visual perception, the visual angle, denoted θ, subtended by a viewed object sometimes looks larger or smaller than its actual value. One approach to this phenomenon posits a subjective correlate to the visual angle: the perceived visual angle or perceived angular size. An optical illusion where the physical and subjective angles differ is then called a visual angle illusion or angular size illusion.Angular size illusions are most obvious as relative angular size illusions, in which two objects that subtend the same visual angle appear to have different angular sizes; it is as if their equal-sized images on the retina were of different sizes. Angular size illusions are contrasted with linear size illusions, in which two objects that are the same physical size do not appear so. An angular size illusion may be accompanied by (or cause) a linear size illusion at the same time.The perceived visual angle paradigm begins with a rejection of the classical size–distance invariance hypothesis (SDIH), which states that the ratio of perceived linear size to perceived distance is a simple function of the visual angle. The SDIH does not explain some illusions, such as the Moon illusion, in which the Moon appears larger when it is near the horizon. It is replaced by a perceptual SDIH, in which the visual angle is replaced by the perceived visual angle. This new formulation avoids some of the paradoxes of the SDIH, but it remains difficult to explain why a given illusion occurs.This paradigm is not universally accepted; many textbook explanations of size and distance perception do not refer to the perceived visual angle, and some researchers deny that it exists. Some recent evidence supporting the idea, reported by Murray, Boyaci and Kersten (2006), suggests a direct relationship between the perceived angular size of an object and the size of the neural activity pattern it excites in the primary visual cortex.