Matt Wolf - CB East Wolf
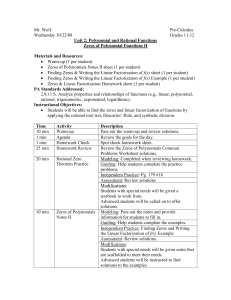
... Step 2) Identify the constant term and the leading coefficient term. List all of the factors of the constant term and put them in a fraction over all of the factors of the leading coefficient term. Constant Term = term without x Leading Coefficient Term = term with greatest exponent of x Factors of ...
... Step 2) Identify the constant term and the leading coefficient term. List all of the factors of the constant term and put them in a fraction over all of the factors of the leading coefficient term. Constant Term = term without x Leading Coefficient Term = term with greatest exponent of x Factors of ...
Sequences and Mathematical Induction
... Base step: P(8) is true because 8¢ can = one 3¢ coin and one 5¢ coin Inductive step: for all integers k ≥ 8, if P(k) is true then P(k+1) is also true Inductive hypothesis: suppose that k is any integer with k ≥ 8: P(k): k¢ can be obtained using 3¢ and 5¢ coins We must show: P(k+1)is true:(k+1)¢ can ...
... Base step: P(8) is true because 8¢ can = one 3¢ coin and one 5¢ coin Inductive step: for all integers k ≥ 8, if P(k) is true then P(k+1) is also true Inductive hypothesis: suppose that k is any integer with k ≥ 8: P(k): k¢ can be obtained using 3¢ and 5¢ coins We must show: P(k+1)is true:(k+1)¢ can ...
Annex B - SEDRIS
... operation. Many spatial operation formulations have closed-form solutions in one direction but do not have closed form solutions for the inverse. This situation leads to a requirement to solve multivariate non-linear equations where no closed solution is readily available. Traditionally, either trun ...
... operation. Many spatial operation formulations have closed-form solutions in one direction but do not have closed form solutions for the inverse. This situation leads to a requirement to solve multivariate non-linear equations where no closed solution is readily available. Traditionally, either trun ...
GigaTensor: Scaling Tensor Analysis Up By 100 Times
... tensors (having attracted best paper awards, e.g. see [20]). However, the toolboxes have critical restrictions: 1) they operate strictly on data that can fit in the main memory, and 2) their scalability is limited by the scalability of Matlab. In [4, 20], efficient ways of computing tensor decomposi ...
... tensors (having attracted best paper awards, e.g. see [20]). However, the toolboxes have critical restrictions: 1) they operate strictly on data that can fit in the main memory, and 2) their scalability is limited by the scalability of Matlab. In [4, 20], efficient ways of computing tensor decomposi ...
Fourier Series
... It is important to establish simple criteria which determine when a Fourier series converges. In this section we will develop conditions on f(x) that enable us to determine the sum of the Fourier series. One quite useful method to analyse the convergence properties is to express the partial sums of ...
... It is important to establish simple criteria which determine when a Fourier series converges. In this section we will develop conditions on f(x) that enable us to determine the sum of the Fourier series. One quite useful method to analyse the convergence properties is to express the partial sums of ...
GigaTensor: Scaling Tensor Analysis Up By 100 Times
... tensors (having attracted best paper awards, e.g. see [22]). However, the toolboxes have critical restrictions: 1) they operate strictly on data that can fit in the main memory, and 2) their scalability is limited by the scalability of Matlab. In [4, 22], efficient ways of computing tensor decomposi ...
... tensors (having attracted best paper awards, e.g. see [22]). However, the toolboxes have critical restrictions: 1) they operate strictly on data that can fit in the main memory, and 2) their scalability is limited by the scalability of Matlab. In [4, 22], efficient ways of computing tensor decomposi ...
Evolving Graph Databases under Description Logic - CEUR
... the semantics of the DL knowledge bases expressing the constraints is defined in terms of interpretations. In turn, graph databases can be naturally seen as finite DL interpretations. Given a set of constraints expressed by a knowledge base K, we have that a (graph) database satisfies the constraint ...
... the semantics of the DL knowledge bases expressing the constraints is defined in terms of interpretations. In turn, graph databases can be naturally seen as finite DL interpretations. Given a set of constraints expressed by a knowledge base K, we have that a (graph) database satisfies the constraint ...
Chapter 5 Preliminaries on Semiparametric Theory and Missing Data Problem
... variates, V , are available, then, they can be used as a surrogate variables in order to gain efficiency. The methodology is also developed for longitudinal data and is presented under a monotone missing data pattern. However, some extensions to arbitrary missing data patterns are also studied. In p ...
... variates, V , are available, then, they can be used as a surrogate variables in order to gain efficiency. The methodology is also developed for longitudinal data and is presented under a monotone missing data pattern. However, some extensions to arbitrary missing data patterns are also studied. In p ...
Spatial Analysis Using ArcGIS 10.1
... 5. Next we must tell the computer whether we are creating a point file, a polyline file, or a polygon file. Choose point file in the ‘Feature Type’ dropdown box. We also have the option to tell the computer the coordinate system we wish the data to be displayed in. 6. Select the edit button. The Spa ...
... 5. Next we must tell the computer whether we are creating a point file, a polyline file, or a polygon file. Choose point file in the ‘Feature Type’ dropdown box. We also have the option to tell the computer the coordinate system we wish the data to be displayed in. 6. Select the edit button. The Spa ...
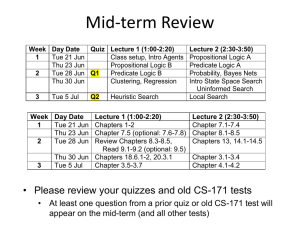
Bayes Net Parameter Learning.
... 3.8 Investigation of Discretization of Network Variables on Predictive Ability of Networks Many data variables used in the study of OSAS are measurements of ...
... 3.8 Investigation of Discretization of Network Variables on Predictive Ability of Networks Many data variables used in the study of OSAS are measurements of ...