Physics 207: Lecture 2 Notes
... ½ m v2 terms are defined to be kinetic energies (A scalar quantity of motion) Physics 207: Lecture 12, Pg 24 ...
... ½ m v2 terms are defined to be kinetic energies (A scalar quantity of motion) Physics 207: Lecture 12, Pg 24 ...
UE1030700 KEplEr`s sEcond law oBJEcTiVE SUMMarY
... The validity of the law of equal areas is not affected by the exact form of the dependence of the central force on the distance from the force centre. This dependence only determines the shape of the orbit around the force centre. Thus, the equal areas law is also valid for the elliptical oscillatio ...
... The validity of the law of equal areas is not affected by the exact form of the dependence of the central force on the distance from the force centre. This dependence only determines the shape of the orbit around the force centre. Thus, the equal areas law is also valid for the elliptical oscillatio ...
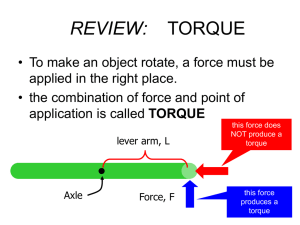
Torque and rotational inertia
... There is another difference between the two. While the result of the dot product is a scalar, the result of the cross product is a vector, meaning it has a direction. So what is the direction of our A x C result? To answer this, you must use the right hand rule for cross products. What you do is th ...
... There is another difference between the two. While the result of the dot product is a scalar, the result of the cross product is a vector, meaning it has a direction. So what is the direction of our A x C result? To answer this, you must use the right hand rule for cross products. What you do is th ...
ME33: Fluid Flow Lecture 1: Information and
... OF FLUID IN PIPELINE Not is steady flow state, consider a control mass comprising the whole of the water in the pipe. By Newton’s Second Law: ...
... OF FLUID IN PIPELINE Not is steady flow state, consider a control mass comprising the whole of the water in the pipe. By Newton’s Second Law: ...
Chapter 3
... 1. If an object is at rest and the net external force acting on it is zero, the object must remain at rest 2. If an object is in motion and the net external force acting on it is zero, the object must continue moving at constant velocity in a straight line 3. If an object is in motion at constant ve ...
... 1. If an object is at rest and the net external force acting on it is zero, the object must remain at rest 2. If an object is in motion and the net external force acting on it is zero, the object must continue moving at constant velocity in a straight line 3. If an object is in motion at constant ve ...
Dynamical Astronomy - University of Glasgow
... B. Gravity assist means that interplanetary missions can be greatly sped up. Y C. Gravity assist can be used to change the direction of the spacecraft and the speed. D. If the planet is moving in the opposite direction to the spacecraft at the time of the fly by, the speed of the spacecraft will not ...
... B. Gravity assist means that interplanetary missions can be greatly sped up. Y C. Gravity assist can be used to change the direction of the spacecraft and the speed. D. If the planet is moving in the opposite direction to the spacecraft at the time of the fly by, the speed of the spacecraft will not ...
Lagrangian Dynamics 2008/09
... 1. Introduction: scope of the course. Newton’s formulation: its strengths and weaknesses. Its relation to 20th Century physics. Inertial frames. Dynamics of a particle: torque, angular momentum, conservation laws. Examples. 2. Dynamics of a system of particles. Central and noncentral forces – the th ...
... 1. Introduction: scope of the course. Newton’s formulation: its strengths and weaknesses. Its relation to 20th Century physics. Inertial frames. Dynamics of a particle: torque, angular momentum, conservation laws. Examples. 2. Dynamics of a system of particles. Central and noncentral forces – the th ...
Vector - DEP
... Displacement is vector quantity :- Aero plane and ship required a fixed direction to go ahead as there are no roads in the sky or in ocean. So distance cover by then is known as displacement , which is vector quantity. Distance is scalar quantity :In roads Bus generally moves according to zig-zag pa ...
... Displacement is vector quantity :- Aero plane and ship required a fixed direction to go ahead as there are no roads in the sky or in ocean. So distance cover by then is known as displacement , which is vector quantity. Distance is scalar quantity :In roads Bus generally moves according to zig-zag pa ...
L11
... Rotational momentum • rotational momentum = moment of inertia angular velocity • since the rotational momentum can’t change then if the moment of inertia changes, the rotational velocity must also change to keep the rotational momentum constant • If the moment of inertia increases, then the rotat ...
... Rotational momentum • rotational momentum = moment of inertia angular velocity • since the rotational momentum can’t change then if the moment of inertia changes, the rotational velocity must also change to keep the rotational momentum constant • If the moment of inertia increases, then the rotat ...
Conservation of Momentum
... A useful analogy for understanding momentum conservation involves a money transaction between two people. Let's refer to the two people as Jack and Jill. Suppose that we were to check the pockets of Jack and Jill before and after the money transaction in order to determine the amount of money which ...
... A useful analogy for understanding momentum conservation involves a money transaction between two people. Let's refer to the two people as Jack and Jill. Suppose that we were to check the pockets of Jack and Jill before and after the money transaction in order to determine the amount of money which ...
Relativistic angular momentum
""Angular momentum tensor"" redirects to here.In physics, relativistic angular momentum refers to the mathematical formalisms and physical concepts that define angular momentum in special relativity (SR) and general relativity (GR). The relativistic quantity is subtly different from the three-dimensional quantity in classical mechanics.Angular momentum is a dynamical quantity derived from position and momentum, and is important; angular momentum is a measure of an object's ""amount of rotational motion"" and resistance to stop rotating. Also, in the same way momentum conservation corresponds to translational symmetry, angular momentum conservation corresponds to rotational symmetry – the connection between symmetries and conservation laws is made by Noether's theorem. While these concepts were originally discovered in classical mechanics – they are also true and significant in special and general relativity. In terms of abstract algebra; the invariance of angular momentum, four-momentum, and other symmetries in spacetime, are described by the Poincaré group and Lorentz group.Physical quantities which remain separate in classical physics are naturally combined in SR and GR by enforcing the postulates of relativity, an appealing characteristic. Most notably; space and time coordinates combine into the four-position, and energy and momentum combine into the four-momentum. These four-vectors depend on the frame of reference used, and change under Lorentz transformations to other inertial frames or accelerated frames.Relativistic angular momentum is less obvious. The classical definition of angular momentum is the cross product of position x with momentum p to obtain a pseudovector x×p, or alternatively as the exterior product to obtain a second order antisymmetric tensor x∧p. What does this combine with, if anything? There is another vector quantity not often discussed – it is the time-varying moment of mass (not the moment of inertia) related to the boost of the centre of mass of the system, and this combines with the classical angular momentum to form an antisymmetric tensor of second order. For rotating mass–energy distributions (such as gyroscopes, planets, stars, and black holes) instead of point-like particles, the angular momentum tensor is expressed in terms of the stress–energy tensor of the rotating object.In special relativity alone, in the rest frame of a spinning object; there is an intrinsic angular momentum analogous to the ""spin"" in quantum mechanics and relativistic quantum mechanics, although for an extended body rather than a point particle. In relativistic quantum mechanics, elementary particles have spin and this is an additional contribution to the orbital angular momentum operator, yielding the total angular momentum tensor operator. In any case, the intrinsic ""spin"" addition to the orbital angular momentum of an object can be expressed in terms of the Pauli–Lubanski pseudovector.