Geometry Yearlong Curriculum Map
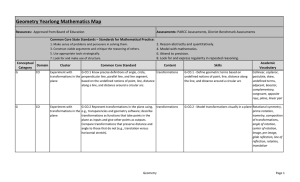
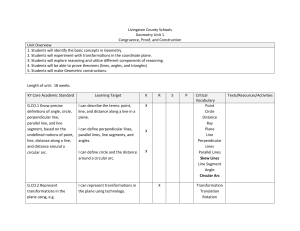
... plane as inputs and give other points as outputs. Compare transformations that preserve distance and angle to those that do not (e.g., translation versus horizontal stretch). Experiment with G-CO.2 Represent transformations in the plane using, transformations transformations in the e.g., transparenc ...
... plane as inputs and give other points as outputs. Compare transformations that preserve distance and angle to those that do not (e.g., translation versus horizontal stretch). Experiment with G-CO.2 Represent transformations in the plane using, transformations transformations in the e.g., transparenc ...
Types of Angles
... What are right, acute, and obtuse angles? How can we use special angle pair definitions to solve for missing angles? How do you classify the different types of triangles by sides? What is the Side-Angle Relationship in triangles? What is the Triangle Inequality Theorem? What does the Triangle Inequa ...
... What are right, acute, and obtuse angles? How can we use special angle pair definitions to solve for missing angles? How do you classify the different types of triangles by sides? What is the Side-Angle Relationship in triangles? What is the Triangle Inequality Theorem? What does the Triangle Inequa ...
4-5 Objective: Prove Triangles Congruent by ASA and AAS
... UTV because they are vertical angles. ...
... UTV because they are vertical angles. ...
Chapters 4.3-4.5 - Ms. Urquhart's Class Page
... Leg: 2 shorter sides of a right triangle Hypotenuse: ...
... Leg: 2 shorter sides of a right triangle Hypotenuse: ...
32 From Galileo to Lorentz transformations
... 32: From Galileo to Lorentz transformations 32.3: Galileo transformations of space-time coordinates and Newtonian mechanics When is an object subject to no force? Experience shows that all known real forces are due to the existence of something which is the source of the force and that the intensit ...
... 32: From Galileo to Lorentz transformations 32.3: Galileo transformations of space-time coordinates and Newtonian mechanics When is an object subject to no force? Experience shows that all known real forces are due to the existence of something which is the source of the force and that the intensit ...
QUANTUM GROUPS AND DIFFERENTIAL FORMS Contents 1
... 1.4. The order of the differential d and N -complexes. Let the field k have characteristic 0. Then, for the basic object Ω(A), the differential d has infinite order, that is, dN = 0 does not hold for any N . And for generic s and q, the same is true for the deformed object Ω(Aq ). However if we choo ...
... 1.4. The order of the differential d and N -complexes. Let the field k have characteristic 0. Then, for the basic object Ω(A), the differential d has infinite order, that is, dN = 0 does not hold for any N . And for generic s and q, the same is true for the deformed object Ω(Aq ). However if we choo ...
Intro to Congruent Figures
... angles of one triangle are __________ congruent to two _______ If _____ two angles of ________ third another triangle, then the ______ ...
... angles of one triangle are __________ congruent to two _______ If _____ two angles of ________ third another triangle, then the ______ ...
Noether's theorem

Noether's (first) theorem states that every differentiable symmetry of the action of a physical system has a corresponding conservation law. The theorem was proven by German mathematician Emmy Noether in 1915 and published in 1918. The action of a physical system is the integral over time of a Lagrangian function (which may or may not be an integral over space of a Lagrangian density function), from which the system's behavior can be determined by the principle of least action.Noether's theorem has become a fundamental tool of modern theoretical physics and the calculus of variations. A generalization of the seminal formulations on constants of motion in Lagrangian and Hamiltonian mechanics (developed in 1788 and 1833, respectively), it does not apply to systems that cannot be modeled with a Lagrangian alone (e.g. systems with a Rayleigh dissipation function). In particular, dissipative systems with continuous symmetries need not have a corresponding conservation law.