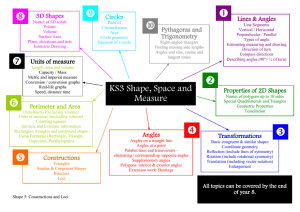
KS3 Shape 5 Constructions and loci 53.77KB
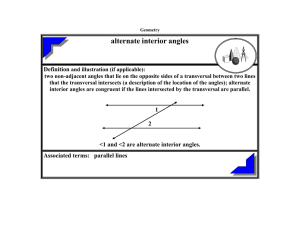
... A kite has just one diagonal which perpendicularly bisects the other. An equilateral triangle has three angles of 60o. It is also important to ensure students are familiar and conversant with the following terms; Perpendicular lines are two lines that meet each other at right angles (90 degrees) Bis ...
... A kite has just one diagonal which perpendicularly bisects the other. An equilateral triangle has three angles of 60o. It is also important to ensure students are familiar and conversant with the following terms; Perpendicular lines are two lines that meet each other at right angles (90 degrees) Bis ...
Date:10/01/2015 UNIT TEST Marks:55
... between their centers. 2) What are the angles in the Major segment? 3) What is the name of a straight line which intersects a circle at two distinct points? 4) The two circles are intersection, what is the maximum number of common tangents to be drawn? 5) What is the distance between the circles of ...
... between their centers. 2) What are the angles in the Major segment? 3) What is the name of a straight line which intersects a circle at two distinct points? 4) The two circles are intersection, what is the maximum number of common tangents to be drawn? 5) What is the distance between the circles of ...
references
... REMARK 1. It is easy to see, that, by virtue of the Fermate theorem, in the condition (3), s0 2 for all r 3. Moreover, in [6], the following nontrivial statement was formulated for the first time: HYPOTHESIS OF NECHAEV. For any m 1, r 2 there exists an infinite set of natural numbers n*(m, r ...
... REMARK 1. It is easy to see, that, by virtue of the Fermate theorem, in the condition (3), s0 2 for all r 3. Moreover, in [6], the following nontrivial statement was formulated for the first time: HYPOTHESIS OF NECHAEV. For any m 1, r 2 there exists an infinite set of natural numbers n*(m, r ...