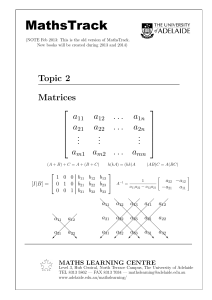
G-inverse and Solution of System of Equations and their
... linear equation determines a line on the xy-plane. Because a solution to a linear system must satisfy all of the equations, the solution set is the intersection of these lines, and is hence either a line, a single point, or the empty set. For three variables, each linear equation determines a plan ...
... linear equation determines a line on the xy-plane. Because a solution to a linear system must satisfy all of the equations, the solution set is the intersection of these lines, and is hence either a line, a single point, or the empty set. For three variables, each linear equation determines a plan ...