![2nd Assignment, due on February 8, 2016. Problem 1 [10], Let G](http://s1.studyres.com/store/data/019737340_1-6b1bb67a45388c2bf632f0c4dc13cf12-300x300.png)
Vector Spaces - Math Berkeley
... Then, we wonder if we can create a natural correspondence somehow between T : V → W and a linear transformation of V ∗ and W ∗ . But given an element f ∈ V ∗ , f : V → Fb , if we wish to associate some g ∈ W ∗ , g : W → Fb , the only way to make function composition work is to map f 7→ f ◦ T −1 . Ho ...
... Then, we wonder if we can create a natural correspondence somehow between T : V → W and a linear transformation of V ∗ and W ∗ . But given an element f ∈ V ∗ , f : V → Fb , if we wish to associate some g ∈ W ∗ , g : W → Fb , the only way to make function composition work is to map f 7→ f ◦ T −1 . Ho ...
Matrice
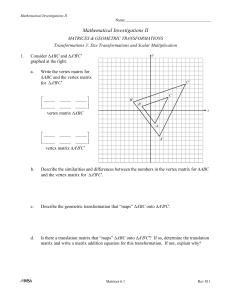
... Given AX = B, we can multiply both sides by the inverse of A, provided this exists, to give A−1AX = A−1B But A−1A = I, the identity matrix. Furthermore, IX = X, because multiplying any matrix by an identity matrix of the appropriate size leaves the matrix ...
... Given AX = B, we can multiply both sides by the inverse of A, provided this exists, to give A−1AX = A−1B But A−1A = I, the identity matrix. Furthermore, IX = X, because multiplying any matrix by an identity matrix of the appropriate size leaves the matrix ...
Notes on Differential Geometry
... Third-order structure: In order to define ridges and valleys, and to analyze how suggestive contours move across a surface, we will need additional notation that describes derivatives of curvature. The gradient ∇κr is a vector in the tangent plane that locally specifies the magnitude and direction ...
... Third-order structure: In order to define ridges and valleys, and to analyze how suggestive contours move across a surface, we will need additional notation that describes derivatives of curvature. The gradient ∇κr is a vector in the tangent plane that locally specifies the magnitude and direction ...