Introduction
... subsets of G, constitute a neighborhood basis of eG^ for the compact open topology. The additive group of a topological vector space is locally quasi-convex if and only if the vector space itself is locally convex, 2]. Therefore it is natural to restrict the duality theory of topological abelian g ...
... subsets of G, constitute a neighborhood basis of eG^ for the compact open topology. The additive group of a topological vector space is locally quasi-convex if and only if the vector space itself is locally convex, 2]. Therefore it is natural to restrict the duality theory of topological abelian g ...
Primitive permutation groups 1 The basics 2
... Any transitive action of a group G is isomorphic to the action by right multiplication on the set of right cosets of a subgroup H of G (where H can be taken to be the stabiliser of a point in the given action). Moreover, the actions on the sets of cosets of two subgroups H and K are isomorphic if an ...
... Any transitive action of a group G is isomorphic to the action by right multiplication on the set of right cosets of a subgroup H of G (where H can be taken to be the stabiliser of a point in the given action). Moreover, the actions on the sets of cosets of two subgroups H and K are isomorphic if an ...
7. Sheaves Definition 7.1. Let X be a topological space. A presheaf
... In other words, we only care about what s looks like in an arbitrarily small neighbourhood of p. Note that when we have a sheaf of rings, the stalk is often a local ring. Example 7.7. Let M be a complex manifold of dimension n and let p be a point of M . Then ...
... In other words, we only care about what s looks like in an arbitrarily small neighbourhood of p. Note that when we have a sheaf of rings, the stalk is often a local ring. Example 7.7. Let M be a complex manifold of dimension n and let p be a point of M . Then ...
Section 18. Continuous Functions - Faculty
... Note. Continuity is the fundamental concept in topology! When you hear that “a coffee cup and a doughnut are topologically equivalent,” this is really a claim about the existence of a certain continuous function (this idea is explored in depth in Chapter 12, “Classification of Surfaces”). We start b ...
... Note. Continuity is the fundamental concept in topology! When you hear that “a coffee cup and a doughnut are topologically equivalent,” this is really a claim about the existence of a certain continuous function (this idea is explored in depth in Chapter 12, “Classification of Surfaces”). We start b ...
Harmonic analysis of dihedral groups
... again a group homomorphism. In other words, the product of two simultaneous eigenfunctions [4] for the translation action of A on L2 (A) is itself a simultaneous eigenfunction. For non-abelian groups, as observed above for dihedral groups G, the notion of simultaneous eigenvector is itself already i ...
... again a group homomorphism. In other words, the product of two simultaneous eigenfunctions [4] for the translation action of A on L2 (A) is itself a simultaneous eigenfunction. For non-abelian groups, as observed above for dihedral groups G, the notion of simultaneous eigenvector is itself already i ...
Pages 7-26 - Rutgers Physics
... the identity is called the order of the symmetry. The order of each of the reflections is 2, the order of C is 4. This set of transformations is called the symmetry group of the square, because it leaves the square shown invariant, although it does permute the four labelled atoms. It is called D4 or ...
... the identity is called the order of the symmetry. The order of each of the reflections is 2, the order of C is 4. This set of transformations is called the symmetry group of the square, because it leaves the square shown invariant, although it does permute the four labelled atoms. It is called D4 or ...
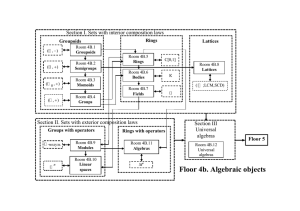
Section I. SETS WITH INTERIOR COMPOSITION LAWS
... We shall consider sets with algebraic structures. Its general notion is composition law. This is an operator, which maps a concrete quality (operation degree) of elements of the given set to an element of this set, for example, addition of numbers, sum of sets. Composition law can be interior and ex ...
... We shall consider sets with algebraic structures. Its general notion is composition law. This is an operator, which maps a concrete quality (operation degree) of elements of the given set to an element of this set, for example, addition of numbers, sum of sets. Composition law can be interior and ex ...
Pseudocompactness and uniform continuity in topological groups
... completion of G, and we reserve the symbol G to denote it. Kister's property U was defined in the summary above. In the same vein, we say that a topological group has property BU if each bounded continuous real-valued function on G is uniformly continuous. The uniform structure on G referred to impl ...
... completion of G, and we reserve the symbol G to denote it. Kister's property U was defined in the summary above. In the same vein, we say that a topological group has property BU if each bounded continuous real-valued function on G is uniformly continuous. The uniform structure on G referred to impl ...
Exam #1 Review
... 14. For rectangles with fixed area, know how to write the perimeter in terms of one side length, and how to determine rectangles with minimum and maximum perimeter. Consider both the case in which the rectangles have integer side lengths as well as the case in which the rectangles need not have int ...
... 14. For rectangles with fixed area, know how to write the perimeter in terms of one side length, and how to determine rectangles with minimum and maximum perimeter. Consider both the case in which the rectangles have integer side lengths as well as the case in which the rectangles need not have int ...
Algebraic Transformation Groups and Algebraic Varieties
... classifying affine G/H by means of its internal geometric structure as a fiber bundle. Cohomological characterizations of affine G/H provide useful vanishing theorems and related information if one already knows G/H is affine. Such characterizations cannot be realistically applied to prove that a given hom ...
... classifying affine G/H by means of its internal geometric structure as a fiber bundle. Cohomological characterizations of affine G/H provide useful vanishing theorems and related information if one already knows G/H is affine. Such characterizations cannot be realistically applied to prove that a given hom ...
Two-dimensional topological field theories and Frobenius - D-MATH
... Definition. A skeleton of a category C is a full subcategory S such that every object in C is isomorphic to exactly one object in S. We know that every oriented closed and connected one-manifold is diffeomorphic to S1 = R/Z. Without loss of generality this diffeomorphism is orientation preserving wi ...
... Definition. A skeleton of a category C is a full subcategory S such that every object in C is isomorphic to exactly one object in S. We know that every oriented closed and connected one-manifold is diffeomorphic to S1 = R/Z. Without loss of generality this diffeomorphism is orientation preserving wi ...
COMPLETE METRIC ABSOLUTE NEIGHBORHOOD RETRACTS 1
... of CW-polytopes. Probably the most well-known is Dugundji-Lefschetz’ theorem about realizations of polytopes. Another result in this spirit is due to Nhu [7]. We introduce a metric property (Property (B) below) which, roughly speaking, says that there is a sequence of maps of CW-polytopes with some ...
... of CW-polytopes. Probably the most well-known is Dugundji-Lefschetz’ theorem about realizations of polytopes. Another result in this spirit is due to Nhu [7]. We introduce a metric property (Property (B) below) which, roughly speaking, says that there is a sequence of maps of CW-polytopes with some ...
http://www.math.uni-muenster.de/u/lueck/publ/lueck/surveyclassi04.pdf
... Let Fn be the free group of rank n. Denote by Out(Fn) the group of outer automorphisms of Fn, i.e. the quotient of the group of all automorphisms of Fn by the normal subgroup of inner automorphisms. Culler and Vogtmann have constructed a space Xn called outer space on which Out(Fn) acts with finite ...
... Let Fn be the free group of rank n. Denote by Out(Fn) the group of outer automorphisms of Fn, i.e. the quotient of the group of all automorphisms of Fn by the normal subgroup of inner automorphisms. Culler and Vogtmann have constructed a space Xn called outer space on which Out(Fn) acts with finite ...
Group action
In mathematics, a symmetry group is an abstraction used to describe the symmetries of an object. A group action formalizes of the relationship between the group and the symmetries of the object. It relates each element of the group to a particular transformation of the object.In this case, the group is also called a permutation group (especially if the set is finite or not a vector space) or transformation group (especially if the set is a vector space and the group acts like linear transformations of the set). A permutation representation of a group G is a representation of G as a group of permutations of the set (usually if the set is finite), and may be described as a group representation of G by permutation matrices. It is the same as a group action of G on an ordered basis of a vector space.A group action is an extension to the notion of a symmetry group in which every element of the group ""acts"" like a bijective transformation (or ""symmetry"") of some set, without being identified with that transformation. This allows for a more comprehensive description of the symmetries of an object, such as a polyhedron, by allowing the same group to act on several different sets of features, such as the set of vertices, the set of edges and the set of faces of the polyhedron.If G is a group and X is a set, then a group action may be defined as a group homomorphism h from G to the symmetric group on X. The action assigns a permutation of X to each element of the group in such a way that the permutation of X assigned to the identity element of G is the identity transformation of X; a product gk of two elements of G is the composition of the permutations assigned to g and k.The abstraction provided by group actions is a powerful one, because it allows geometrical ideas to be applied to more abstract objects. Many objects in mathematics have natural group actions defined on them. In particular, groups can act on other groups, or even on themselves. Despite this generality, the theory of group actions contains wide-reaching theorems, such as the orbit stabilizer theorem, which can be used to prove deep results in several fields.