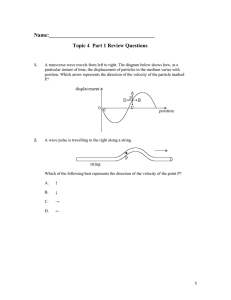
Momentum and Collisions
... Find the final velocity of the train of three carts. (b) What If ? Does your answer require that all the carts collide and stick together at the same time? What if they collide in a different ...
... Find the final velocity of the train of three carts. (b) What If ? Does your answer require that all the carts collide and stick together at the same time? What if they collide in a different ...
Teaching ideas for Topic 2: Mechanics, Core
... 32 on page 61 of the textbook and the example on page 56. They are well worth discussing in detail in class. It is important to stress that ‘equilibrium’ means ‘motion with constant speed on a straight line’ but that the speed could be zero. It must be stressed to students, therefore, that if they h ...
... 32 on page 61 of the textbook and the example on page 56. They are well worth discussing in detail in class. It is important to stress that ‘equilibrium’ means ‘motion with constant speed on a straight line’ but that the speed could be zero. It must be stressed to students, therefore, that if they h ...
Name - westlake-science
... 23. What force is responsible for the orbits of the planets in the solar system? 24. When shooting an arrow at a target, why is it advisable to aim above the bull’s-eye rather than directly at it? 25. When a tennis player practices by hitting a ball against a wall, which of Newton’s laws of motion i ...
... 23. What force is responsible for the orbits of the planets in the solar system? 24. When shooting an arrow at a target, why is it advisable to aim above the bull’s-eye rather than directly at it? 25. When a tennis player practices by hitting a ball against a wall, which of Newton’s laws of motion i ...
Friction - WordPress.com
... 2. Alex leaves a book at rest on his desk. 3. Two teams of students are playing tug of war. One team is stronger than the other and pulls the rope with twice as much force as the other team. 4. A kid is in a swimming pool. He pushes on the side of the pool and accelerates away from the side. ...
... 2. Alex leaves a book at rest on his desk. 3. Two teams of students are playing tug of war. One team is stronger than the other and pulls the rope with twice as much force as the other team. 4. A kid is in a swimming pool. He pushes on the side of the pool and accelerates away from the side. ...
Newton’s Laws of Motion
... Think about a fish swimming in water. A fish uses its fins to push water backwards. In turn, the water reacts by pushing the fish forwards, propelling the fish through the water. The size of the force on the water equals the size of the force on the fish. The direction of the force on the water (bac ...
... Think about a fish swimming in water. A fish uses its fins to push water backwards. In turn, the water reacts by pushing the fish forwards, propelling the fish through the water. The size of the force on the water equals the size of the force on the fish. The direction of the force on the water (bac ...
Work and Energy_ppt_RevW10
... • First Law: Objects continue their state of motion (rest or constant velocity) unless acted upon by a net external force. • Second Law: The action of a net external force on an object is to cause its momentum to change with time. For objects with a constant mass this can be written as F = ma. • Thi ...
... • First Law: Objects continue their state of motion (rest or constant velocity) unless acted upon by a net external force. • Second Law: The action of a net external force on an object is to cause its momentum to change with time. For objects with a constant mass this can be written as F = ma. • Thi ...
Newton`s 2nd law problems
... Need to find acceleration first, F = ma 168 = 8.7a A = 19.3 m/s2 then solve acceleration for time a = (v-vo)/ t t = (v-vo) /a (8-0)/19.3 = 0.41 sec ...
... Need to find acceleration first, F = ma 168 = 8.7a A = 19.3 m/s2 then solve acceleration for time a = (v-vo)/ t t = (v-vo) /a (8-0)/19.3 = 0.41 sec ...
Newtons First Law
... motion unless acted on by an outside force. An object at rest tends to stay at rest unless acted on by an outside force. Also known as inertia ...
... motion unless acted on by an outside force. An object at rest tends to stay at rest unless acted on by an outside force. Also known as inertia ...
Newton's theorem of revolving orbits
In classical mechanics, Newton's theorem of revolving orbits identifies the type of central force needed to multiply the angular speed of a particle by a factor k without affecting its radial motion (Figures 1 and 2). Newton applied his theorem to understanding the overall rotation of orbits (apsidal precession, Figure 3) that is observed for the Moon and planets. The term ""radial motion"" signifies the motion towards or away from the center of force, whereas the angular motion is perpendicular to the radial motion.Isaac Newton derived this theorem in Propositions 43–45 of Book I of his Philosophiæ Naturalis Principia Mathematica, first published in 1687. In Proposition 43, he showed that the added force must be a central force, one whose magnitude depends only upon the distance r between the particle and a point fixed in space (the center). In Proposition 44, he derived a formula for the force, showing that it was an inverse-cube force, one that varies as the inverse cube of r. In Proposition 45 Newton extended his theorem to arbitrary central forces by assuming that the particle moved in nearly circular orbit.As noted by astrophysicist Subrahmanyan Chandrasekhar in his 1995 commentary on Newton's Principia, this theorem remained largely unknown and undeveloped for over three centuries. Since 1997, the theorem has been studied by Donald Lynden-Bell and collaborators. Its first exact extension came in 2000 with the work of Mahomed and Vawda.