Newton`s Laws of Motion
... not moving, the coin will land at your feet when you drop it. Where will it land if the bus is moving in a straight line at constant speed? It will fall in the same spot as if the bus wasn't moving. This is because once the bus is moving at a constant velocity, the coin is also moving at the velocit ...
... not moving, the coin will land at your feet when you drop it. Where will it land if the bus is moving in a straight line at constant speed? It will fall in the same spot as if the bus wasn't moving. This is because once the bus is moving at a constant velocity, the coin is also moving at the velocit ...
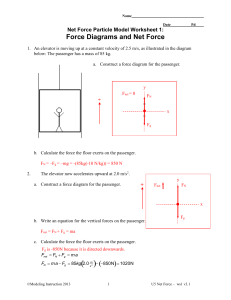
Force Diagrams and Net Force Key
... System C has the greatest net force. FN and Fg cancel out for the block moving horizontally. All of the "FT"s cancel out inside the systems because each string is pulling equally in both directions. The net force on each system is the force of gravity on the hanging masses. System C has the heaviest ...
... System C has the greatest net force. FN and Fg cancel out for the block moving horizontally. All of the "FT"s cancel out inside the systems because each string is pulling equally in both directions. The net force on each system is the force of gravity on the hanging masses. System C has the heaviest ...
Research Papers-Astrophysics/Download/2244
... With the equations (3.6.a.b.c), we found the accelerations of the gyrotational part of gravitomagnetism, that work upon a satellite in a circular orbit about the Earth, whereby the satellite’s orbit plane is under an angle with the Earth’s equator. Obliviously, none of the accelerations is zero, thu ...
... With the equations (3.6.a.b.c), we found the accelerations of the gyrotational part of gravitomagnetism, that work upon a satellite in a circular orbit about the Earth, whereby the satellite’s orbit plane is under an angle with the Earth’s equator. Obliviously, none of the accelerations is zero, thu ...
Causes of circular motion
... centripetal acceleration is determined from the free-body diagram (tension, gravity, friction, normal force, etc). Since F=ma and ac=v2/r, the magnitude of the centripetal force equals mv2/r or, written together, Fc=mv2/r. The direction of the centripetal force is the same as the centripetal acc ...
... centripetal acceleration is determined from the free-body diagram (tension, gravity, friction, normal force, etc). Since F=ma and ac=v2/r, the magnitude of the centripetal force equals mv2/r or, written together, Fc=mv2/r. The direction of the centripetal force is the same as the centripetal acc ...
Chapter 6: Forces
... The acceleration of an object as produced by a net force is directly proportional to the magnitude of the net force, in the same direction as the net force, and inversely proportional to the mass of the object. ...
... The acceleration of an object as produced by a net force is directly proportional to the magnitude of the net force, in the same direction as the net force, and inversely proportional to the mass of the object. ...
Physics 220 – Exam #1
... vy zero and the acceleration along y negative. The y direction is vertical, and the “positive” direction is “up”. ...
... vy zero and the acceleration along y negative. The y direction is vertical, and the “positive” direction is “up”. ...
Question Paper and Solution (Eng)
... David, initially at P, walks towards east for 20 minutes. He then walks towards south for 15 minutes and reaches Q. In the whole journey, his speed is 2 m s1. What is the time needed if he walks with a speed of 3 ms-1 from Q back to P along a straight line? ...
... David, initially at P, walks towards east for 20 minutes. He then walks towards south for 15 minutes and reaches Q. In the whole journey, his speed is 2 m s1. What is the time needed if he walks with a speed of 3 ms-1 from Q back to P along a straight line? ...
Newton`s First Law
... Let’s start with an easy one, your weight. Remember that weight is relative – your mass isn’t changing (the amount of matter in you) but you weigh different amounts because of gravity Gravity’s acceleration is 9.8m/s2 On earth you take your weight to be what it is ...
... Let’s start with an easy one, your weight. Remember that weight is relative – your mass isn’t changing (the amount of matter in you) but you weigh different amounts because of gravity Gravity’s acceleration is 9.8m/s2 On earth you take your weight to be what it is ...
C-Circular-Kinematics-Dynamics-Unit
... 3. analyze the angular displacement and angular velocity of a rotating object. 4. analyze and calculate torque. 5. analyze rotational equilibrium. 6. analyze moment of inertia. 7. analyze angular momentum and the relationship between moment of inertia and rotational speed. 8. asses qualitatively and ...
... 3. analyze the angular displacement and angular velocity of a rotating object. 4. analyze and calculate torque. 5. analyze rotational equilibrium. 6. analyze moment of inertia. 7. analyze angular momentum and the relationship between moment of inertia and rotational speed. 8. asses qualitatively and ...
Newton's theorem of revolving orbits
In classical mechanics, Newton's theorem of revolving orbits identifies the type of central force needed to multiply the angular speed of a particle by a factor k without affecting its radial motion (Figures 1 and 2). Newton applied his theorem to understanding the overall rotation of orbits (apsidal precession, Figure 3) that is observed for the Moon and planets. The term ""radial motion"" signifies the motion towards or away from the center of force, whereas the angular motion is perpendicular to the radial motion.Isaac Newton derived this theorem in Propositions 43–45 of Book I of his Philosophiæ Naturalis Principia Mathematica, first published in 1687. In Proposition 43, he showed that the added force must be a central force, one whose magnitude depends only upon the distance r between the particle and a point fixed in space (the center). In Proposition 44, he derived a formula for the force, showing that it was an inverse-cube force, one that varies as the inverse cube of r. In Proposition 45 Newton extended his theorem to arbitrary central forces by assuming that the particle moved in nearly circular orbit.As noted by astrophysicist Subrahmanyan Chandrasekhar in his 1995 commentary on Newton's Principia, this theorem remained largely unknown and undeveloped for over three centuries. Since 1997, the theorem has been studied by Donald Lynden-Bell and collaborators. Its first exact extension came in 2000 with the work of Mahomed and Vawda.