Newton`s Second Law: Acceleration
... Newton’s second law states that the acceleration produced by a net force on an object • Is directly proportional to the magnitude of the net force, • is in the same direction as the net force, and • is inversely proportional to the mass of the object ...
... Newton’s second law states that the acceleration produced by a net force on an object • Is directly proportional to the magnitude of the net force, • is in the same direction as the net force, and • is inversely proportional to the mass of the object ...
Tri 3 Study Guide 2014
... o What is the result of unbalanced and balanced forces acting on an object? Balanced forces: ________________________________________________________ Unbalanced forces: ______________________________________________________ ...
... o What is the result of unbalanced and balanced forces acting on an object? Balanced forces: ________________________________________________________ Unbalanced forces: ______________________________________________________ ...
Chapter 2 Summary
... comparing their predictions with experiments by Galileo and others • Reworked ideas until they described motion of everything studied up to his time • Laws applied to celestial motion as well as terrestrial motion • Others used the Laws to make predictions that ...
... comparing their predictions with experiments by Galileo and others • Reworked ideas until they described motion of everything studied up to his time • Laws applied to celestial motion as well as terrestrial motion • Others used the Laws to make predictions that ...
Set 4 - UCF Physics
... different approach. For years they fought over who was the real inventor! ...
... different approach. For years they fought over who was the real inventor! ...
13.1-4 Spring force and elastic energy revisited. (Hooke’s law)
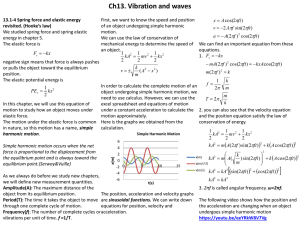
... When two waves are out of phase the final We define following new physical quantities. displacement is difference between the two Wavelength(λ) waves. m Distance between two successive points that x https://youtu.be/uKrvTA4SKVU behave identically. Then from the frequency equation, T 2 ...
... When two waves are out of phase the final We define following new physical quantities. displacement is difference between the two Wavelength(λ) waves. m Distance between two successive points that x https://youtu.be/uKrvTA4SKVU behave identically. Then from the frequency equation, T 2 ...
Honors Work, Energy
... =1680J Note work done by gravity is + b/c it is helping with motion • Also- be careful with the angle - usually we measure angle between F and D but in this case the angle given was the incline angle ...
... =1680J Note work done by gravity is + b/c it is helping with motion • Also- be careful with the angle - usually we measure angle between F and D but in this case the angle given was the incline angle ...
10 - San Diego Mesa College
... in the gap between the dees also alternates. The dees are also immersed in a uniform magnetic field directed perpendicularly to them. A source of ions is provided at the center. These ions are accelerated as they enter the gap, and go into circular orbits with a fixed period given above. If the peri ...
... in the gap between the dees also alternates. The dees are also immersed in a uniform magnetic field directed perpendicularly to them. A source of ions is provided at the center. These ions are accelerated as they enter the gap, and go into circular orbits with a fixed period given above. If the peri ...
Newton's theorem of revolving orbits
In classical mechanics, Newton's theorem of revolving orbits identifies the type of central force needed to multiply the angular speed of a particle by a factor k without affecting its radial motion (Figures 1 and 2). Newton applied his theorem to understanding the overall rotation of orbits (apsidal precession, Figure 3) that is observed for the Moon and planets. The term ""radial motion"" signifies the motion towards or away from the center of force, whereas the angular motion is perpendicular to the radial motion.Isaac Newton derived this theorem in Propositions 43–45 of Book I of his Philosophiæ Naturalis Principia Mathematica, first published in 1687. In Proposition 43, he showed that the added force must be a central force, one whose magnitude depends only upon the distance r between the particle and a point fixed in space (the center). In Proposition 44, he derived a formula for the force, showing that it was an inverse-cube force, one that varies as the inverse cube of r. In Proposition 45 Newton extended his theorem to arbitrary central forces by assuming that the particle moved in nearly circular orbit.As noted by astrophysicist Subrahmanyan Chandrasekhar in his 1995 commentary on Newton's Principia, this theorem remained largely unknown and undeveloped for over three centuries. Since 1997, the theorem has been studied by Donald Lynden-Bell and collaborators. Its first exact extension came in 2000 with the work of Mahomed and Vawda.