Momentum and Impulse
... 12) A baseball pitcher claims he can throw a 0.145 kg baseball with as much momentum as a speeding bullet. Assume that a 3.00 g bullet moves at a speed of 1.5x103 m/s. What must the baseball's speed be if the pitcher is correct? ...
... 12) A baseball pitcher claims he can throw a 0.145 kg baseball with as much momentum as a speeding bullet. Assume that a 3.00 g bullet moves at a speed of 1.5x103 m/s. What must the baseball's speed be if the pitcher is correct? ...
Chapter 4 - Equilibrium of Particle
... - Tension always acts in the direction of the cable - Tension force in a continuous cable must have a constant magnitude for equilibrium ...
... - Tension always acts in the direction of the cable - Tension force in a continuous cable must have a constant magnitude for equilibrium ...
ParticleSystems - Computer Science and Engineering
... The example system we showed at the beginning had a fixed number of particles In practice, we want to be able to create and destroy particles on the fly Often times, we have a particle system that generates new particles at some rate The new particles are given initial properties according to some c ...
... The example system we showed at the beginning had a fixed number of particles In practice, we want to be able to create and destroy particles on the fly Often times, we have a particle system that generates new particles at some rate The new particles are given initial properties according to some c ...
Ch. 8. Energy
... Jupiter, as it has the greatest value of g. It would weigh the least on the Moon. 23. If an object weighs 400 N, what is its mass ? Mass = Weight / g = 400 / 10 = 40 kg 24. What happens when a net force acts on an object ? Its velocity or state of rest changes. The object accelerates. 25. If no net ...
... Jupiter, as it has the greatest value of g. It would weigh the least on the Moon. 23. If an object weighs 400 N, what is its mass ? Mass = Weight / g = 400 / 10 = 40 kg 24. What happens when a net force acts on an object ? Its velocity or state of rest changes. The object accelerates. 25. If no net ...
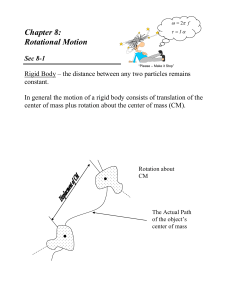
Chapter 8: Rotational Motion
... How to “think” about Torque 1. Torque must be specified about a pivot point 2. Torque is a product quantity made up of distance and force. 3. Torque causes angular acceleration, , in the same way that forces cause linear accelerations. 4. The Moment of Inertia, I, is a measure of resistance to rota ...
... How to “think” about Torque 1. Torque must be specified about a pivot point 2. Torque is a product quantity made up of distance and force. 3. Torque causes angular acceleration, , in the same way that forces cause linear accelerations. 4. The Moment of Inertia, I, is a measure of resistance to rota ...
Chapter 7 Notes - Valdosta State University
... and jumps into a 12.0 kg sled initially at rest. If friction is negligible, find the velocity of the sled and person as they move away. If the person and sled coast 30.0 m before coming to rest, find the coefficient of friction between the sled and the ground. A ballistic pendulum is a device which ...
... and jumps into a 12.0 kg sled initially at rest. If friction is negligible, find the velocity of the sled and person as they move away. If the person and sled coast 30.0 m before coming to rest, find the coefficient of friction between the sled and the ground. A ballistic pendulum is a device which ...
Solutions to Physics 110 Sample Mid-Term Exam (hand
... A9) The angular velocity decreases. If the merry-go-round is rotating freely with a constant angular velocity, then it has an angular momentum which is L = I ω, where I is the rotational moment of inertia and ω is the angular velocity. Once you step onto the merry-go-round at a distance r from the c ...
... A9) The angular velocity decreases. If the merry-go-round is rotating freely with a constant angular velocity, then it has an angular momentum which is L = I ω, where I is the rotational moment of inertia and ω is the angular velocity. Once you step onto the merry-go-round at a distance r from the c ...
P4 – Explaining Motion
... 1. Identify forces arising from an interaction between two objects 2. Identify the ‘partner’ of a given force (i.e. the other force of the interaction pair) 3. Specify, for each force, the object which exerts it, and the object on which it acts 4. Use arrows to show the sizes and directions of ...
... 1. Identify forces arising from an interaction between two objects 2. Identify the ‘partner’ of a given force (i.e. the other force of the interaction pair) 3. Specify, for each force, the object which exerts it, and the object on which it acts 4. Use arrows to show the sizes and directions of ...
South Pasadena · AP Chemistry
... 54. The force of air resistance acting on an elephant, compared to the force of air resistance acting on a feather is . . a) greater for the elephant The effect of the air resistance is greater on the feather because it is lighter in weight, but the value is greater for the elephant because it is mu ...
... 54. The force of air resistance acting on an elephant, compared to the force of air resistance acting on a feather is . . a) greater for the elephant The effect of the air resistance is greater on the feather because it is lighter in weight, but the value is greater for the elephant because it is mu ...
4 Newton`s Second Law of Motion
... – The acceleration of an object is directly proportional to the net force acting on the object, is in the direction of the net force, and is inversely proportional to the mass of the object. – a = Fnet/m; a: acceleration produced by the net force (m/s2), Fnet : the net force (N), m: the mass of the ...
... – The acceleration of an object is directly proportional to the net force acting on the object, is in the direction of the net force, and is inversely proportional to the mass of the object. – a = Fnet/m; a: acceleration produced by the net force (m/s2), Fnet : the net force (N), m: the mass of the ...
4.3 Newton`s Second Law of Motion
... 2. A force that acts at a distance (not touching), such as gravity, the magnetic force, or the electric force. These are called field forces. They are invisible and were not discovered/understood until “modern” times – late 1800’s. © 2010 Pearson Education, Inc. ...
... 2. A force that acts at a distance (not touching), such as gravity, the magnetic force, or the electric force. These are called field forces. They are invisible and were not discovered/understood until “modern” times – late 1800’s. © 2010 Pearson Education, Inc. ...
Third Midterm Exam Solutions
... Problem 4 (20 points): A diver comes off a board with arms straight up and legs straight down, giving her a moment of inertia about her rotation axis of Ii = 18 kg·m2 . She then tucks into a small ball, decreasing this moment of inertia to If = 3.6 kg·m2 . While tucked, she makes two complete revol ...
... Problem 4 (20 points): A diver comes off a board with arms straight up and legs straight down, giving her a moment of inertia about her rotation axis of Ii = 18 kg·m2 . She then tucks into a small ball, decreasing this moment of inertia to If = 3.6 kg·m2 . While tucked, she makes two complete revol ...
Circular Motion
... (horizontal). Estimate the force a person must exert on a string attached to a 0.150-kg ball to make the ball revolve in a horizontal circle of radius 0.600 m. The ball makes 2.00 revolutions per second. Ignore the string’s mass. ...
... (horizontal). Estimate the force a person must exert on a string attached to a 0.150-kg ball to make the ball revolve in a horizontal circle of radius 0.600 m. The ball makes 2.00 revolutions per second. Ignore the string’s mass. ...
Newton's theorem of revolving orbits
In classical mechanics, Newton's theorem of revolving orbits identifies the type of central force needed to multiply the angular speed of a particle by a factor k without affecting its radial motion (Figures 1 and 2). Newton applied his theorem to understanding the overall rotation of orbits (apsidal precession, Figure 3) that is observed for the Moon and planets. The term ""radial motion"" signifies the motion towards or away from the center of force, whereas the angular motion is perpendicular to the radial motion.Isaac Newton derived this theorem in Propositions 43–45 of Book I of his Philosophiæ Naturalis Principia Mathematica, first published in 1687. In Proposition 43, he showed that the added force must be a central force, one whose magnitude depends only upon the distance r between the particle and a point fixed in space (the center). In Proposition 44, he derived a formula for the force, showing that it was an inverse-cube force, one that varies as the inverse cube of r. In Proposition 45 Newton extended his theorem to arbitrary central forces by assuming that the particle moved in nearly circular orbit.As noted by astrophysicist Subrahmanyan Chandrasekhar in his 1995 commentary on Newton's Principia, this theorem remained largely unknown and undeveloped for over three centuries. Since 1997, the theorem has been studied by Donald Lynden-Bell and collaborators. Its first exact extension came in 2000 with the work of Mahomed and Vawda.