CP-S-HW-ch-8-detailed
... object is in equilibrium if the forces are equal in magnitude and opposite in direction. (b) The object is in equilibrium if the net torque on the object is zero. (c) The object is in equilibrium if the forces act at the same point on the object. (d) The object is in equilibrium if the net force and ...
... object is in equilibrium if the forces are equal in magnitude and opposite in direction. (b) The object is in equilibrium if the net torque on the object is zero. (c) The object is in equilibrium if the forces act at the same point on the object. (d) The object is in equilibrium if the net force and ...
Lecture 06: Conservation of Angular Momentum
... A sphere mass m1 and a block of mass m2 are connected by a light cord that passes over a pulley. The radius of the pulley is R, and the mass of the thin rim is M. The spokes of the pulley have negligible mass. The block slides on a ...
... A sphere mass m1 and a block of mass m2 are connected by a light cord that passes over a pulley. The radius of the pulley is R, and the mass of the thin rim is M. The spokes of the pulley have negligible mass. The block slides on a ...
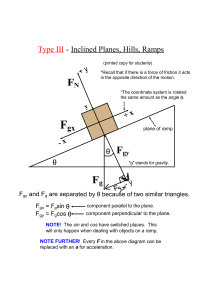
Type III Inclined Planes, Hills, Ramps
... *Recall that if there is a force of friction it acts in the opposite direction of the motion. *The coordinate system is rotated the same amount as the angle θ. ...
... *Recall that if there is a force of friction it acts in the opposite direction of the motion. *The coordinate system is rotated the same amount as the angle θ. ...
Chapter 2
... More about rotational mass: • Rotational mass of an object measures how difficult to change its angular velocity. The value of rotational mass depends on the ordinary mass of the object and its distribution around the specific rotational axis. • The contribution of each portion of mass of an object ...
... More about rotational mass: • Rotational mass of an object measures how difficult to change its angular velocity. The value of rotational mass depends on the ordinary mass of the object and its distribution around the specific rotational axis. • The contribution of each portion of mass of an object ...
Name
... What two things can you say about an object’s motion if the net forces on the object are zero? Which of these objects are accelerating? a. A ball that is falling. b. A rocket flying at a constant velocity through space. c. A car traveling down the road at a constant velocity. d. A book resting on a ...
... What two things can you say about an object’s motion if the net forces on the object are zero? Which of these objects are accelerating? a. A ball that is falling. b. A rocket flying at a constant velocity through space. c. A car traveling down the road at a constant velocity. d. A book resting on a ...
Forces and the Laws of Motion
... 3) Draw and label vector arrows for all external forces acting on the object. ...
... 3) Draw and label vector arrows for all external forces acting on the object. ...
Chapter 6
... • A force is nonconservative if the work it does on an object depends on the path taken by the object between its final and starting points. • Examples of nonconservative forces: kinetic friction, air drag, propulsive forces • For friction force, the work required is less on the blue path than on th ...
... • A force is nonconservative if the work it does on an object depends on the path taken by the object between its final and starting points. • Examples of nonconservative forces: kinetic friction, air drag, propulsive forces • For friction force, the work required is less on the blue path than on th ...
14_2spr_121E2
... skier who is a vertical distance 4.00 m above the bottom of the incline. There is some friction present, µ = 0.100. Since you can't walk up the incline, you give the box a push that gives it an initial velocity; then the box slides up the incline, slowing down under the forces of friction and gravit ...
... skier who is a vertical distance 4.00 m above the bottom of the incline. There is some friction present, µ = 0.100. Since you can't walk up the incline, you give the box a push that gives it an initial velocity; then the box slides up the incline, slowing down under the forces of friction and gravit ...
Mrs
... _____ 82. The weight of fluid displaced by a floating object is equal to the weight of the object. _____ 83. Pressure in a fluid is inversely proportional to the depth at which the pressure measurement is taken. _____ 84. The buoyant force on a submerged rock depends on the volume of the rock. _____ ...
... _____ 82. The weight of fluid displaced by a floating object is equal to the weight of the object. _____ 83. Pressure in a fluid is inversely proportional to the depth at which the pressure measurement is taken. _____ 84. The buoyant force on a submerged rock depends on the volume of the rock. _____ ...
EOC_chapter7 - AppServ Open Project 2.4.9
... spring. Assume that the needle has mass 5.60 g, the light spring has force constant 375 N/m, and the spring is originally compressed 8.10 cm to project the needle horizontally without friction. After the needle leaves the spring, the tip of the needle moves through 2.40 cm of skin and soft tissue, w ...
... spring. Assume that the needle has mass 5.60 g, the light spring has force constant 375 N/m, and the spring is originally compressed 8.10 cm to project the needle horizontally without friction. After the needle leaves the spring, the tip of the needle moves through 2.40 cm of skin and soft tissue, w ...
Calculating the height your rocket will reach . rocket has
... Up to this point we would use the following equation to calculate the height reached by an accelerating object: ...
... Up to this point we would use the following equation to calculate the height reached by an accelerating object: ...
From last time… - High Energy Physics
... Electrical Energy • Electricity is the flow of charged particles. • Charged particles have an electromagnetic force between them similar to the gravitational force. • This force can do work. • Doing work against this force can store energy in the system. • The energy can be removed at any time to d ...
... Electrical Energy • Electricity is the flow of charged particles. • Charged particles have an electromagnetic force between them similar to the gravitational force. • This force can do work. • Doing work against this force can store energy in the system. • The energy can be removed at any time to d ...
AP Physics B Exam Cram Sheet
... 33. In N3, the reaction force is always the same kind of force as the first one (the reaction to a frictional force is another frictional force, the reaction to a gravitational force is another gravitational force). 34. The Law of Conservation of Momentum is based on the action-reaction pair of forc ...
... 33. In N3, the reaction force is always the same kind of force as the first one (the reaction to a frictional force is another frictional force, the reaction to a gravitational force is another gravitational force). 34. The Law of Conservation of Momentum is based on the action-reaction pair of forc ...
Classical central-force problem
In classical mechanics, the central-force problem is to determine the motion of a particle under the influence of a single central force. A central force is a force that points from the particle directly towards (or directly away from) a fixed point in space, the center, and whose magnitude only depends on the distance of the object to the center. In many important cases, the problem can be solved analytically, i.e., in terms of well-studied functions such as trigonometric functions.The solution of this problem is important to classical physics, since many naturally occurring forces are central. Examples include gravity and electromagnetism as described by Newton's law of universal gravitation and Coulomb's law, respectively. The problem is also important because some more complicated problems in classical physics (such as the two-body problem with forces along the line connecting the two bodies) can be reduced to a central-force problem. Finally, the solution to the central-force problem often makes a good initial approximation of the true motion, as in calculating the motion of the planets in the Solar System.