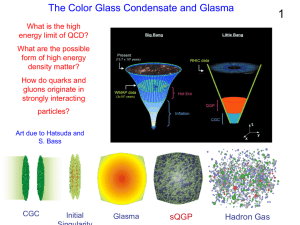
Elementary Treatment The ground state of hydrogen atom has been
... where |E20 | is the unperturbed energy in n = 2 state Z8ae0 . Clearly the 200 state has lower energy that 21m state. Thus, the first order correction not only removes the ` degeneracy but also gives the result that lower angular momentum states have lower energy. Identical Particles We have seen the ...
... where |E20 | is the unperturbed energy in n = 2 state Z8ae0 . Clearly the 200 state has lower energy that 21m state. Thus, the first order correction not only removes the ` degeneracy but also gives the result that lower angular momentum states have lower energy. Identical Particles We have seen the ...
Exam Results - University of Wisconsin–Madison
... determined. • There is an equivalent relation in the time and energy domain. – Einstein's relation that space and time or momentum and mass/energy are similar. ...
... determined. • There is an equivalent relation in the time and energy domain. – Einstein's relation that space and time or momentum and mass/energy are similar. ...
Quantum Reality
... most tightly bound inner atomic orbit, making chemistry and also life impossible. We owe our very existence to the Fermi-Dirac statistics of electrons.” ...
... most tightly bound inner atomic orbit, making chemistry and also life impossible. We owe our very existence to the Fermi-Dirac statistics of electrons.” ...
Atomic Physics
... If Rutherford’s model is correct, the accelerating electrons will lose energy continuously, then they will be adhered to the nucleus and all atoms will finally be collapsed! ...
... If Rutherford’s model is correct, the accelerating electrons will lose energy continuously, then they will be adhered to the nucleus and all atoms will finally be collapsed! ...
The Zero-Point Field and the NASA Challenge to Create the Space
... A similar experience of equal and opposite forces arises in the process of accelerating (pushing on) an object that is free to move. It is an experimental fact that to accelerate an object, a force must be applied by an agent and that the agent will thus experience an equal and opposite reaction for ...
... A similar experience of equal and opposite forces arises in the process of accelerating (pushing on) an object that is free to move. It is an experimental fact that to accelerate an object, a force must be applied by an agent and that the agent will thus experience an equal and opposite reaction for ...
The de Broglie-Bohr Model for the Hydrogen Atom
... This figure shows that atomic stability involves a balance between potential and kinetic energy. The electron is drawn toward the nucleus by the attractive potential energy interaction (~ -1/R), but is prevented from collapsing into the nucleus by the extremely large kinetic energy (~1/R 2) associa ...
... This figure shows that atomic stability involves a balance between potential and kinetic energy. The electron is drawn toward the nucleus by the attractive potential energy interaction (~ -1/R), but is prevented from collapsing into the nucleus by the extremely large kinetic energy (~1/R 2) associa ...
Renormalization

In quantum field theory, the statistical mechanics of fields, and the theory of self-similar geometric structures, renormalization is any of a collection of techniques used to treat infinities arising in calculated quantities.Renormalization specifies relationships between parameters in the theory when the parameters describing large distance scales differ from the parameters describing small distances. Physically, the pileup of contributions from an infinity of scales involved in a problem may then result in infinities. When describing space and time as a continuum, certain statistical and quantum mechanical constructions are ill defined. To define them, this continuum limit, the removal of the ""construction scaffolding"" of lattices at various scales, has to be taken carefully, as detailed below.Renormalization was first developed in quantum electrodynamics (QED) to make sense of infinite integrals in perturbation theory. Initially viewed as a suspect provisional procedure even by some of its originators, renormalization eventually was embraced as an important and self-consistent actual mechanism of scale physics in several fields of physics and mathematics. Today, the point of view has shifted: on the basis of the breakthrough renormalization group insights of Kenneth Wilson, the focus is on variation of physical quantities across contiguous scales, while distant scales are related to each other through ""effective"" descriptions. All scales are linked in a broadly systematic way, and the actual physics pertinent to each is extracted with the suitable specific computational techniques appropriate for each.